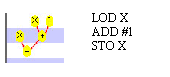Correction de la série d'exercices no 2

Exercice 2-1 : Scanning, parsing,code generation

(x + (4 + y)) * (x + y)

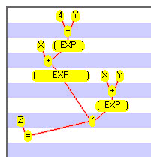
1 + (2 * (1 + (2 * (1 + x))))

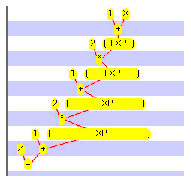
x * y + z

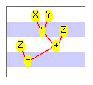
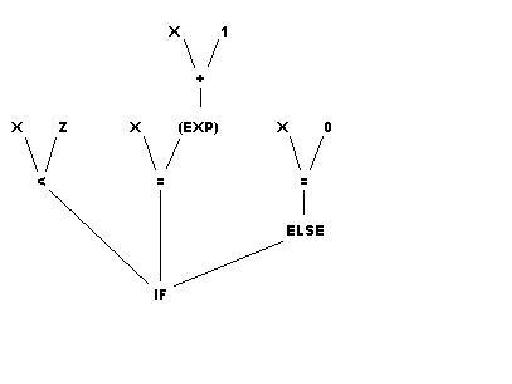
if (x < z) x = x + 1 else x = 0

Exercice 2-2 : Scanning, parsing,code generation

1. x += 1 <=> x = x + 1
• Scanning:
"x" => ident; "=" => assign op; "x" => variable; "+" => plus op; "1" => number

• Parsing and code generation:
  

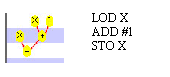
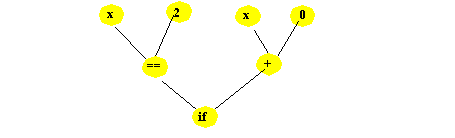
2. if (x == 2) x = 0
• Scanning:
"if" => token if; "(" => token left brace; "x" => ident; "==" comparison op
"2" => number; ")" => token right brace; "x" => ident; "=" assign op; "0" => number

• Parsing:


• Code Generation:

[0] LOD #2 ; charge le chiffre 2 dans l'accumulateur
[2] SUB X ; soustrait X à l'accumulateur (2 - X dans l'accumulateur)
[4] STO T1 ; stocke le résultat dans la cellule T1 (2 - X dans la cellule T1, T1 est une cellule temporaire)
[6] CPZ T1; teste 2 - X == 0 (si c'est vrai, met 1 dans l'accumulateur, si c'est faux, met 0 dans l'accumulateur)
[8] JMZ 14 ; si le contenu de l'accumulateur est 0, saute à l'instruction [14], sinon va à l'instruction suivante
[10] LOD #0 ; charge le chiffre 0 dans l'accumulateur
[12] STO X ; stocke le contenu de l'accumulateur dans la cellule X (0 dans la cellule X)
[14] HLT


Exercice 2-3 : Binary logic et tableaux booléens

a	b	a AND b
0	0	0
0	1	0
1	0	0
1	1	1




a	b	a OR b
0	0	0
0	1	1
1	0	1
1	1	1




a	NOT a
0	1
1	0



1. a1 = a <=> a AND 1 = 1
   

   a	b	a AND b
   0	1	0
   1	1	1

   
   
2. a * (a + b) = a <=> a AND (a OR b) = a
   

   a	b	Z = a OR b	a AND Z
   0	0	0	0
   0	1	1	0
   1	0	1	1
   1	1	1	1

   
   
3. (ab)' = a' + b' <=> NOT (a AND b) = (NOT a) OR (NOT b)
   

   a	b	Z = a AND b	NOT Z
   0	0	0	1
   0	1	0	1
   1	0	0	1
   1	1	1	0

   
   

   a	b	NOT a OR NOT b
   0	0	1
   0	1	1
   1	0	1
   1	1	0

   
   

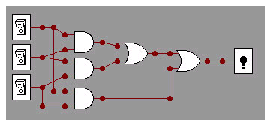
Exercice 2-4 : Binary logic et portes logiques

1. Circuit AND (NOT (a OR NOT b)) :
   
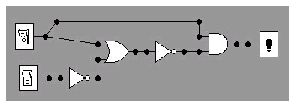
2. Circuit majorité :