Cet exercice est une introduction à la complexité des problèmes.
Il existe (N-1)! possibilités de connecter les N villes. Attention, comme le problème est symmétrique (Le trajet de la ville A à la ville B est identique en longueur au trajet de la ville B à la ville A), on ne peut retenir que la moitié des possibilités. Au final, il y a donc (N-1)! / 2 différents chemins entre les N villes.
Voici un algorithme qui permet de répondre au problème :
% The cities (nodes) are numbered N={1,2,...,n}.
% w(i,j) is the length of the path (edge) between cities i and j.
% w is the total length of a given path between k cities.
% S is a variable that includes
% as a first argument the number k of cities in the path
% as a second argument a partial path (ordered list of k integers in square brackets),
% as the last argument the total length of this partial path.
% The initial path to try is the incomplete path with only 1 city [1].
% New cities will be added.
% Once all n cities are touched, the path will be compared to an initial best S
which is [1,2,...n] with total length w(1,2)+w(2,3)+...+w(n-1,n).
% The algorithm is a recursive function. It will make (n-1)! calls to itself to search all possible paths.
|
|
w = w(1,2) + w(2,3) + w(3,4) + ... + w(n-1,n) + w(n,1) Best_S_so_far = ( n, [ 1, 2, 3, ... , n-1, n ], w ) S = ( 1, [ 1 ], 0 ) Search( S, Best_S_so_far ) print Best_S_so_far |
% Length initial best S % Construct initial best S % Initial path to try % Search all paths iteratively for better S % Print result |
procedure Search( S, Best_S_so_far )
let ( k, [ i1, i2, ... , ik ], w ) = S
let ( n, [ i1B, i2B, ... , inB ], wB ) = Best_S_so_far
if k = n then
new_w = w + w(ik,i1)
if new_w < wB then
Best_S_so_far = ( k, [ i1, i2, ... , ik ], new_w )
end if
else
for all j not in [ i1, i2, ... , ik ]
new_w = w + w(ik,j)
New_S = ( k+1, [ i1, i2, ... , ik, j ], new_w )
Search( New_S, Best_S_so_far )
end for
endif
return
end
|
% we have a full path % make the cycle complete % If the new solution is better than the % previous, keep it, otherwise continue % Incomplete path: % add a branch... % and call search again % ...for all cities not in current path |

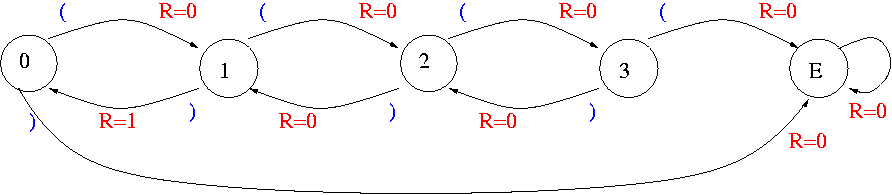
Pour que la machine fonctionne correctement, elle doit être dans l'état '1' lorsqu'elle lit le premier caractère.