Correction des Exercices serie 5

Correction de la série d'exercices no 5

Exercice 5-1 : Turing machine - codage

a. Machine de Turing :

111	Marquage du début du tableau
0100101000100	(1, 1, 1, b, R) *
11	Séparation entre 2 règles
010101000100	(1, 0, 1, b, R) *
11	Séparation entre 2 règles
01000101000100	(1, b, 1, b, R) *
111	Marquage de la fin du tableau
* (Etat présent, Symbole présent, Nouvel état, Nouveau symbole, Mouvement)

Codage utilisé :

États
Le nombre de zeros est le numéro de l'état.
Symboles
0	0
00	1
000	b
Mouvement
0	L
00	R

Cette machine efface le ruban à droite de sa position initiale. Elle ne s'arrête jamais...

b. pour exercice 5.5. Machine de Turing universelle :

Z	Marquage du début du tableau
(1, 1, 1, b, R)*	001x1x001xbxR
Y	Séparation entre 2 règles
(1, 0, 1, b, R)*	001x0x001xbxR
Y	Séparation entre 2 règles
(1, b, 1, b, R)*	001xbx001xbxR
Z	Marquage de la fin du tableau
* (Etat présent, Symbole présent, Nouvel état, Nouveau symbole, Mouvement)

Codage utilisé :

États
La valeur décimale du chiffre binaire est le numéro de l'état.
Symboles
0	0
1	1
b	b
Mouvement
L	L
R	R

Exercice 5-2 : Turing machine - parenthesis checker

Contrairement à la machine à états finis de la semaine passée, il est ici possible de généraliser la machine de Turing pour un nombre arbitraire de jeu de parenthèses. En effet, le ruban d'une machine de Turing est de taille infinie. Une mémoire de taille infinie est donc à disposition sur le ruban.

Il existe plusieurs solutions à ce problème. Une des solutions possibles est l'algorithme suivant :

Etat 1 : Recherche de la première parenthèse ouverte en allant à droite
1. S'il n'y en a pas (arrivée à la fin de l'expression) -> stop avec '1' (signifie que l'expression était juste)
2. S'il y en a une -> passage à l'état 2
3. S'il y a une parenthèse fermante (l'expression commence par ')' ) -> stop avec '0'
Etat 2 : Recherche de la première parenthèse fermée en allant à droite
1. S'il n'y en a pas (arrivée à la fin de l'expression) -> stop avec '0' (signifie que l'expression n'était pas correcte)
2. S'il y en a une -> passage à l'état 3
Etat 3 : Recherche de la parenthèse ouverte suivante en allant à gauche
1. S'il n'y en a plus (arrivée à la fin de l'expression) -> stop avec '1' (signifie que l'expression était juste)
2. S'il y en a une -> passage à l'état 2

Attention, à chaque fois qu'une parenthèse est rencontrée, elle doit être marquée pour pas être comptée plusieurs fois.

On peut facilement convertir cet algorithme en une machine de Turing. Les conventions suivantes sont utilisées :

Un '!' marque le début et la fin de l'expression
Chaque parenthèse rencontrée est remplacée par un X
L'alphabet de la machine est {( ) X !}

Voici les règles de jeu. Elles reprennent presque littéralement l'algorithme donné ci-dessus à quelques différences près.
Un état supplémentaire de départ est nécessaire. (L'état de départ est obligatoirement 1 dans notre applet.) Il vérifie que l'expression commence avec un '!', à savoir que l'on se trouve bien au début de l'expression et s'arrête avec une erreur si ce n'est pas le cas.
Les états 1-3 dans l'algorithme ci-dessus sont donc représentés par les états 2-4 dans la machine ci-dessous.
L'état 5 est un état d'arrêt.

Machine de Turing pour la vérification de suites de parenthèses
Règle #	Etat courant	Entrée	Etat suivant	Ecrit sur ruban	Mouvement	Commentaire
1.	1	(	5	E	R	État de départ
2.	1	)	5	E	R
3.	1	X	5	E	R
4.	1	!	2	X	R
5.	2	(	3	X	R	Cherche ( en allant à droite
6.	2	)	5	0	R
7.	2	X	2	X	R
8.	2	!	5	1	L
9.	3	(	3	(	R	Cherche ) en allant à droite
10.	3	)	4	X	L
11.	3	X	3	X	R
12.	3	!	5	0	L
13.	4	(	3	X	R	Cherche ( en allant à gauche
14.	4	)	4	)	L
15.	4	X	4	X	L
16.	4	!	2	!	R

Exercice 5-3 : Problème de `Halting'

( voir nouvelle version de l'ennoncé de la serie 5 ) Supposons H dit que le programme nP=2387 s'arrête pour l'entrée nX=2387. Alors D entre dans une boucle infinie et l'entree sur la diagonale dans la table construite avec H est fausse pour n=2387.

Exercice 5-4a : Problèmes de décidabilité

Un problème décidable est un problème qui peut être résolu par une procédure pas à pas, systématique. Décidable a le même sens que calculable.
Un problème de décision est un problème dont la réponse ne peut être que oui ou non.
Décider si un problème est décidable ou non décidable n'est pas évident sans une définition précise du problème à résoudre. Quelques-uns des cas ci-dessous peuvent être soit décidables, soit non-décidables dépendant de la formulation du problème. Par exemple, le problème de carrelage est décidable pour des espaces finis, mais pas décidable dans le cas général.

	Décidable	de Décision
Halting problem Vérification qu'un programme A appliqué à une entrée X se termine	non	oui
Tri d'une liste de chaînes de charactères	oui	non
Vérification de programme Vérification qu'un programme A peut résoudre un problème P	non	oui
Tiling problem Vérification que l'on peut couvrir à partir d'un nombre fini de différents types de carreaux un espace infini	non	oui
Nombre premier Vérification si un nombre est premier ou non	oui	oui
Problème du voyageur de commerce Recherche du chemin le plus court reliant N villes (N est un nombre fini)	oui	non

Exercice 5-4 : Réflexion sur la décidabilité et l'intelligence

Il y a quelques remarques que l'on peut faire par rapport à ce que dit cet étudiant.
Une propriété essentielle du cerveau humain est la créativité. C'est ce qui entre autre nous distingue d'un ordinateur. Cette remarque est donc valable. Par contre, il n'est pas entièrement correct de dire qu'un cerveau est plus puissant qu'un ordinateur. Par exemple, une tâche très simple comme approximer 22 / 7 avec une précision de 10 décimales est une tâche difficile pour l'homme. La puissance d'un instrument dépend donc toujours du problème qu'il essaie de résoudre.
Cependant, la puissance de calcul n'est pas la caractéristique qui distingue l'homme de la machine.

Cela dit, il n'est pas possible de déterminer pour n'importe quel programme s'il converge ou non (halting problem). Le fait de démontrer qu'un programme SPECIFIQUE s'arrête ne suffit pas. La tâche algorithmique est de le déterminer pour n'importe quel programme, soit pour TOUTES LES ENTREES LEGALES. Or il n'existe pas de tel algorithme. Par exemple, on peut facilement montrer que le chiffre 14358 n'est pas une nombre premier, mais cela ne veut pas dire qu'on a résolu le problème algorithmique de dire pour chaque nombre s'il est premier ou non. Similairement, on peut montrer que le programme suivant s'arrête.

 		
			x=3
	  		set x=x-2
	  		if x=1 then
	  		stop

Mais on ne peut pas montrer pour n'importe quel programme s'il s'arrête ou non.

Finalement, la déclaration de cet étudiant contient des idées intéressantes, mais globalement, elle n'est pas correcte.

Exercice 5-5 : Codage sur ruban pour machine de Turing universelle

voir 5.1. b

Exercice 5-6; Machine de Turing universelle - partie `adress finder'.

( voir nouvelle version de l'ennoncé de la serie 5 ) En utilisant le schema de la machine `adress finder' au tableau, suivre l'action de la machine sur le ruban suivant:

S110x1ZY000x1x111x1x1Y100x1x111x1x1Y110x1x111x1x1Z

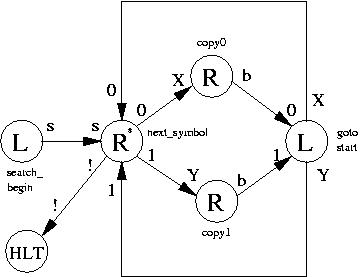
La position initiale de la tête de lecture est sur le premier Z.
L'état initial est l'état L toute à gauche sur le graph au tableau.

La machine bouge a gauche en remplacent les 0 et 1 par A et B jusqu'au début marqué par un S.
SBBAxBZY000x1x111x1x1Y100x1x111x1x1Y110x1x111x1x1Z
Elle bouge a gauche, trouve un B, le remplace par un 1 et transit vers l'état de la branche basse du graph.
S1BAxBZY000x1x111x1x1Y100x1x111x1x1Y110x1x111x1x1Z
Elle trouve un 0 ce qui indique que le premier bit de l'adresse n'est pas correct. Alors elle continu à droite jusqu'au Y. Elle retourne à gauche en remplacant tous les 0 et 1 par A et B.
SBBAxBZYAAAxBxBBBxBxBY100x1x111x1x1Y110x1x111x1x1Z
Elle recommence à lire le premier bit de l'adresse et remplace le B par un 1. En allant vers la droite elle ignora tous les A et B, alors ells s'accroche à la 2e règle (après le Y), trouve et 1 ce qui est correct et le remplace par un B.
S1BAxBZYAAAxBxBBBxBxBYB00x1x111x1x1Y110x1x111x1x1Z
Ensuite elle retourne à S sans changement du ruban.
Maintenant elle lit le 2e bit de l'adresse. Le B sera remplace par le 1, et elle cherche un 1. Mais le premier bit (en ignorant les A et B) est un zero. Alors, elle remplace tous les 0 et 1 de cette règle par des A et B.
SBBAxBZYAAAxBxBBBxBxBYBAAxBxBBBxBxBY110x1x111x1x1Z
Dans le prochain tour elle trouvera la bonne règle. Quand l'adresse est trouvée, une autre machine peut commencer à copier.

Exercice 5-7 : Turing machine - copie d'une séquence

Voici une possibilité de machine à états finis. Nous vous donnons ici sa représentation schématique.

Une machine de copie est l'une des deux machines nécessaires pour construire une machine de Turing universelle. L'autre est une machine de recherche des adresses (address finding machine).