
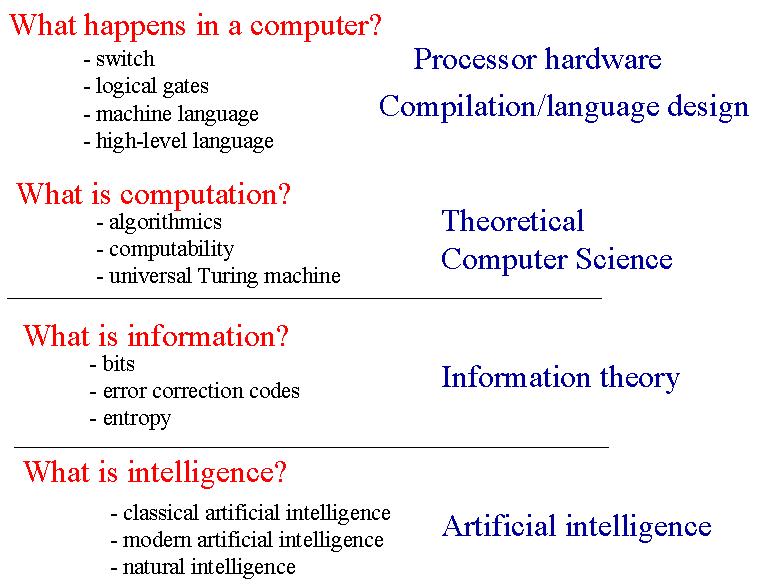
Ce cours n'est pas un cours de programmation, mais un cours qui a pour but de vous introduire aux fondements du "Computer Science". Ce cours se décline en 4 parties qui tentent de répondre aux 4 questions suivantes :
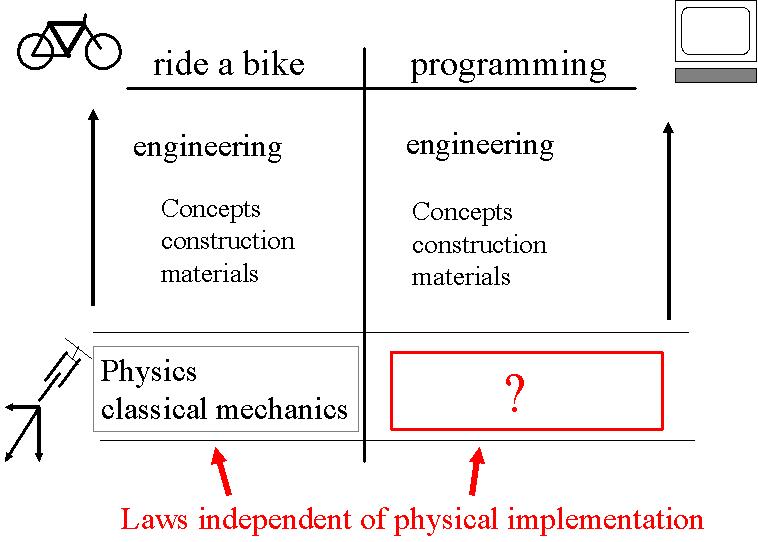
Par analogie avec un enfant qui a appris à faire du vélo, mais qui ne connaît
pas forcément les lois physiques qui lui permettent de rouler, vous avez appris à
programmer sans forcément connaître ou comprendre les lois du "Computer Science"
qui permettent d'écrire et de faire tourner des programmes informatiques.
Ce sont les concepts du "computer science" ci-dessus que nous allons tenter de vous faire découvrir.



Les concepts du "computer science" et les questions qui en sont à la base sont essentielles, parce qu'elles sont proches des questions qui touchent le cerveau humain, son fonctionnement, celui de la pensée, de la conscience, et de l'intelligence.
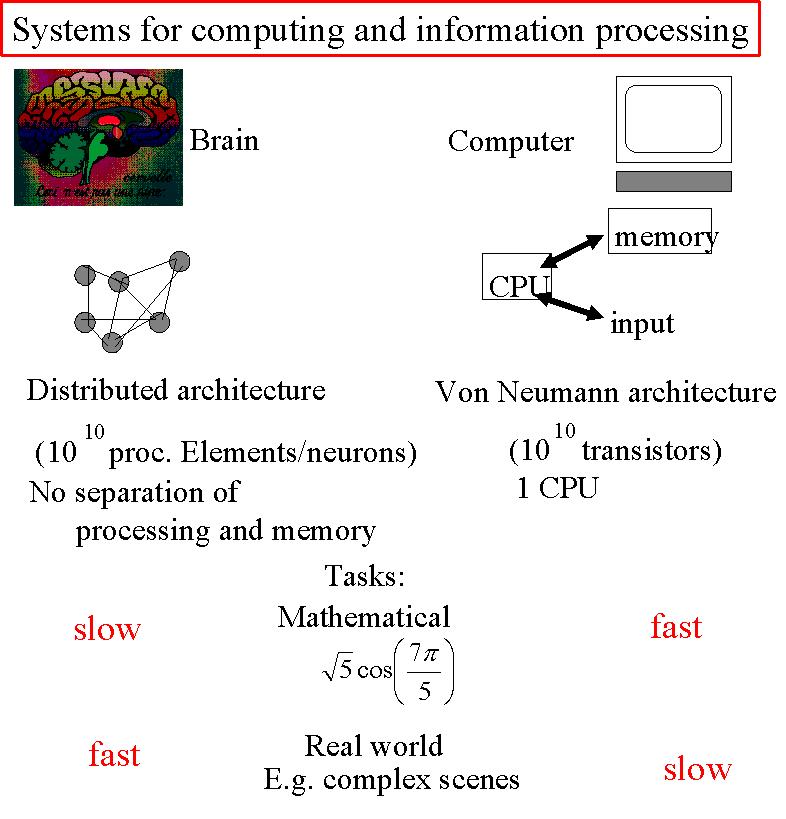
Le cerveau et l'ordinateur présentent de nombreuses similitudes, mais également
de nombreuses différences.
En effet, tout deux sont constitués
d'unités élémentaires (neurones vs transistors) qui définissent une architecture
particulière (architecture distribuée vs architecture Von Neumann). Le cerveau présente une connectivité
impressionnante. Il est organisé de
façon tridimensionnelle, sans séparation de la mémoire et du "processing", ce qui n'est pas le cas
pour l'ordinateur.
Les unités élémentaires y existent en quantités
égales, autorisant en théorie la même capacité de calcul pour le cerveau comme pour l'ordinateur.
Cependant, il est clair que ce n'est pas aussi simple. Par exemple, les tâches complexes, nécessitant un temps
de "processing" relativement long ne sont pas les mêmes pour le cerveau et l'ordinateur, et le temps nécessaire à
leur traitement est différent en fonction des tâches demandées.
D'où l'importance du questionnement lié au "computer science".
Le "computer science" est né à partir de l'algèbre et de la logique. Charles Babbage (1821) a été le premier à proposer une machine capable d'exécuter certains algorithmes, mais il aura fallu attendre 1930 et Zuse, Atanasoff et Aiken pour découvrir le premier ordinateur efficace.
A l'origine de n'importe quel ordinateur (Sun, PC, PIPPIN) et quel que soit le langage de programmation employé, il y a le code machine. Le code binaire en est la base.
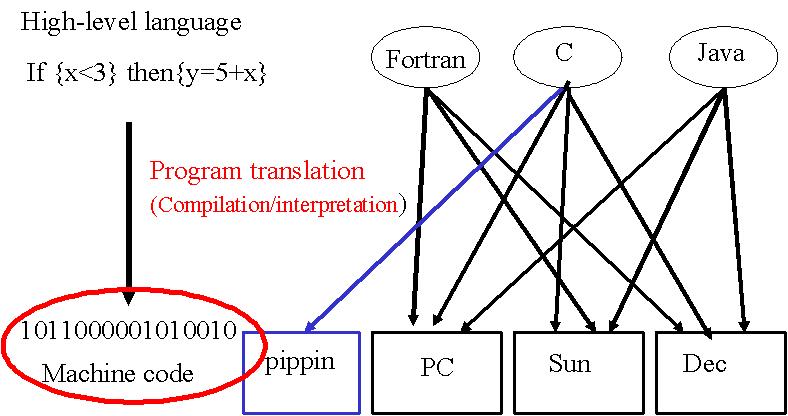
Le code binaire (constitué de 0 et de 1) est simple à utiliser et permet de construire des structures plus complexes, telles que des switches, des mémoires, etc.
Nous allons voir comment représenter un chiffre, une image ou un texte selon un code binaire. En réalité, on peut représenter presque n'importe quoi à l'aide de ce code, par exemple le son, les instructions données à un ordinateur, etc.
A chaque code binaire correspond un nombre décimal et inversément. Il est important de savoir passer d'une forme à l'autre.

Le code hexadécimal repose sur le code binaire. C'est un code constitué d'une série de 4 bits. Ces 4 bits autorisent 24 = 16 configurations différentes, correspondant à 16 caractères différents (0,1,2,...,9,A,B,C,...,F)

Une image est une succession de pixels.
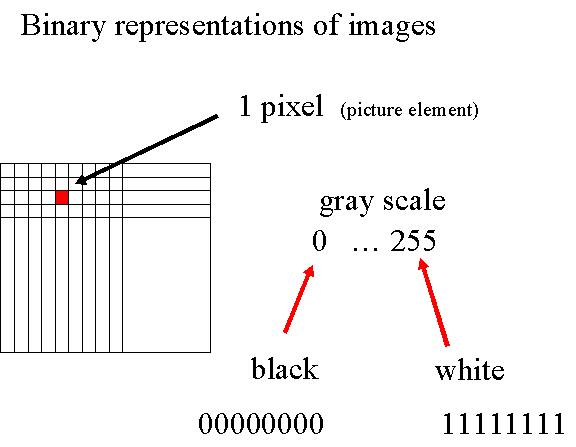
Chaque pixel d'une image noir-blanc est le plus souvent codé sur 8 bits. Ces 8 bits permettent 28 = 256 niveaux de gris différents. 00000000 est le code pour le noir, 11111111 pour le blanc, les valeurs de code intermédiaires codant pour les divers gris. Ces différents gris sont définis par leur valeur binaire (ou décimale). En effet, le changement des bits les plus à droite ne vont entraîner qu'une faible variation de gris, puisqu'ils n'induisent qu'une faible variation de la valeur binaire. Le changement des bits les plus à gauche par contre vont entraîner une variation élevée de la valeur binaire, donc une variation importante de la teinte de gris.

Il est possible de coder les pixels d'une image avec moins de 8 bits, par ex 4 bits. Ces 4 bits autorisent 24 = 16 tons de gris différents. L'image résultante ne peut alors pas présenter autant de tonalité que précédemment.

On peut même coder les pixels avec seulement 1 bit. L'image ne sera alors faite que de points strictement noirs ou blancs.

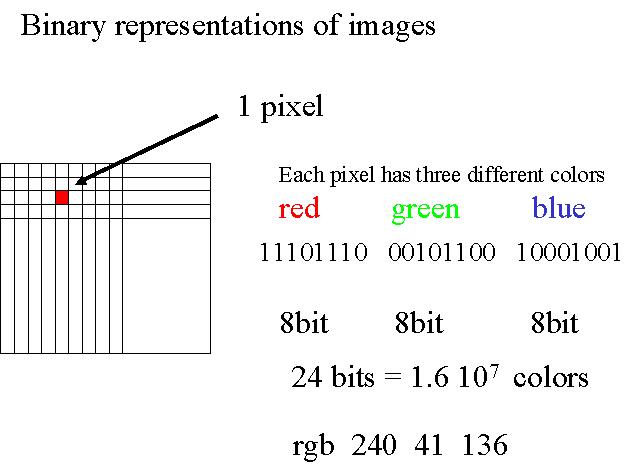
Considérons maintenant une image en couleur. Chaque pixel d'une telle image est en général codée
par 3 fois 8 bits (24 bits). Les huit premiers bits, selon le même principe que précédemment, codent pour la couleur
rouge, les 8 suivants pour le vert, les 8 derniers pour le bleu. Les 28 = 256 différentes valeurs que peuvent prendre les
8 bits déterminent les différents tons de rouge, vert ou bleu, et le mélange des trois couleurs donne la couleur
finale du pixel désiré. On parle du code RGB pour RED GREEN BLUE.
Afin de faciliter la lecture de ce code, on l'exprime le plus souvent en code décimal, c'est-à-dire
avec 3 nombres, ou en code hexadécimal, c'est-à-dire avec 3 fois 2
caractères (2 caractères par couleur).

Voici ce que pourrait donner une image pour laquelle nous n'aurions que les 8 premiers bits, ceux codant pour le rouge.

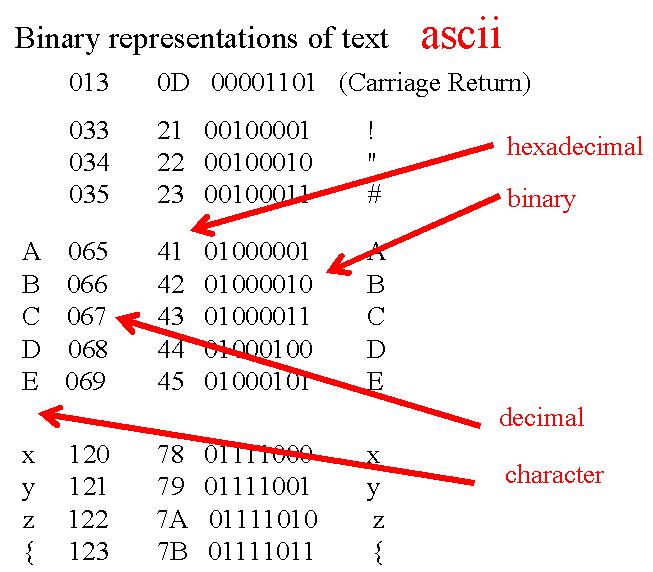
Il a été défini une convention pour le codage des caractères de texte. Cette convention a été nommée le code ASCII. Elle associe à chaque caractère une valeur décimale entre 0 et 255, ainsi que les valeurs hexadécimales (2 caractères hexa) et binaires (sur 8 bits) correspondantes. Malheureusement, ce code n'est pas entièrement standardisé.
On peut modéliser un ordinateur hypothétique très simple qu'on nommera PIPPIN à l'aide d'une mémoire qui permet de stocker un certain nombre d'informations et d'un accumulateur qui permet de procéder à certaines tâches.
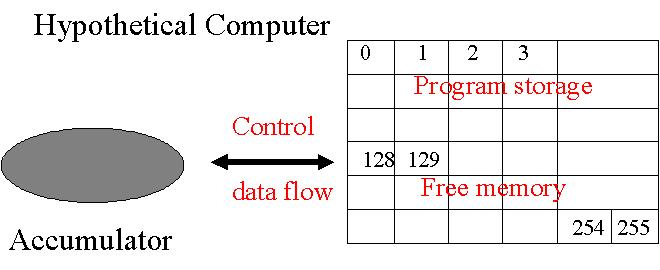
On définit plusieurs commandes que l'accumulateur peut effectuer. Par exemple, LOD (abréviation pour
LOAD) qui permet d'aller chercher en mémoire une information et de la placer dans l'accumulateur pour usage ultérieur,
ou encore STO
(abréviation pour STORE) qui permet de stocker l'information contenue dans l'accumulateur en mémoire.
Ces commandes sont codées avec 8 bits.
Voici quelques commandes existantes.

On organise ensuite la mémoire sous forme de cellules qui peuvent stocker une information. On donne à
chacune de ces cellules une adresse codée par 8 autres bits.
On peut enfin donner une suite d'instructions permettant de manipuler des informations, exècuter des algorithmes, etc.
En voici un court exemple :
X=2 is stored in cell memory 129 Y=3 is stored in cell memory 130 W is stored in cell memory 128 W = X + Y Programme: [0]LOD X --> LOD 129 [2]ADD Y --> ADD 130 [4]STO W --> STO 128 [6]HLT
[0]LOD X --> 00000100 10000001 [2]ADD Y --> 00000000 10000010 [4]STO W --> 00000101 10000000 [6]HLT --> 00001111 00000000
Le "high-level language" est le langage formé par une suite d'instructions telle que nous aurions pu l'écrire dans un programme C.
diff=c-d; if(diff == 0) diff=-1;
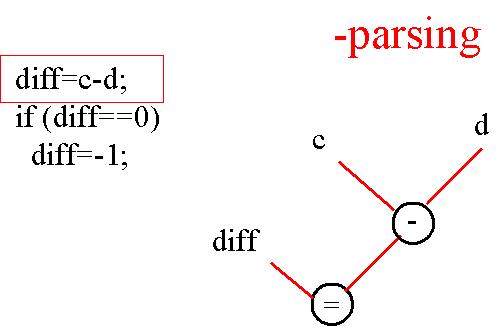
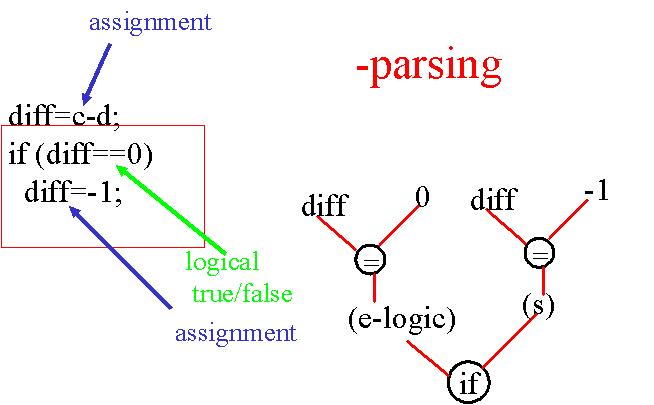
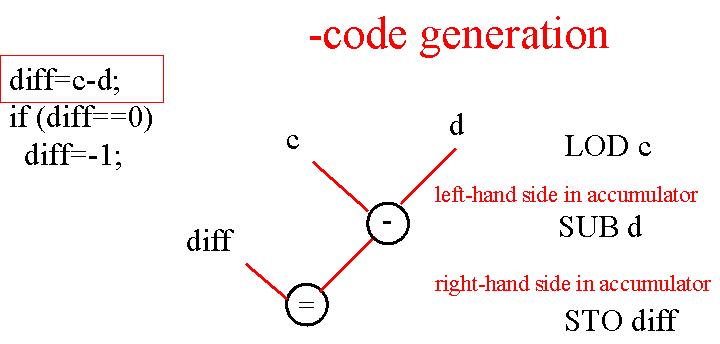
Voilà décrite l'étape de traduction entre le langage de haut niveau (JAVA, C, etc.), et le langage assembleur.
Dans le programme C ci-dessus, l'ordinateur doit sélectionner certaines instructions, par exemple LOAD ou ADD. Pour cela, il doit posséder des interrupteurs pour lui permettre de "switcher" entre ces différentes instructions.
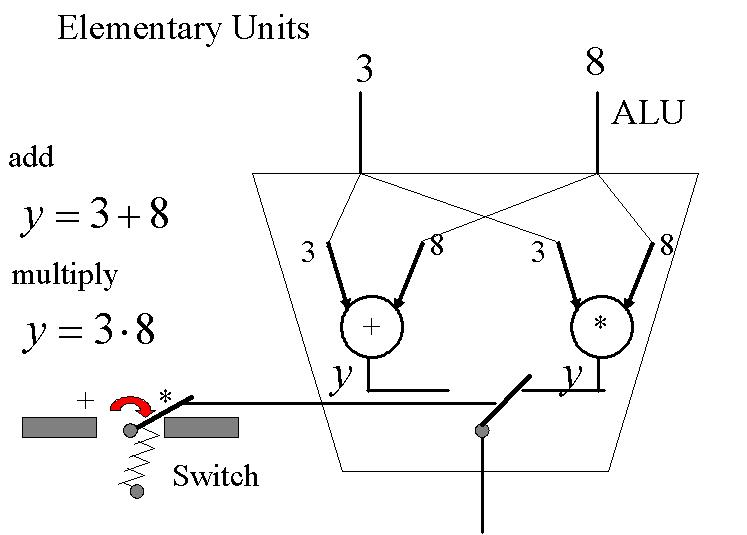
N'importe quel interrupteur peut être créé à partir des portes logiques et des 3 tableaux booléens ci-dessous.
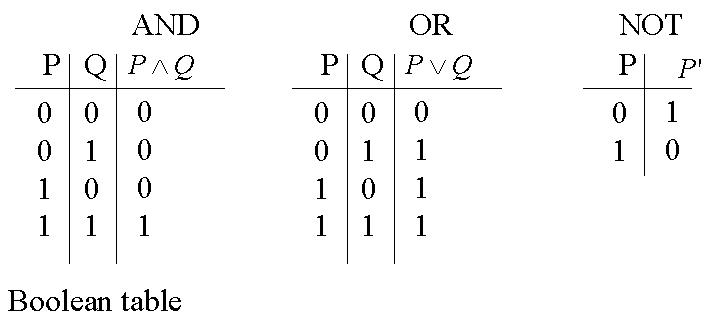
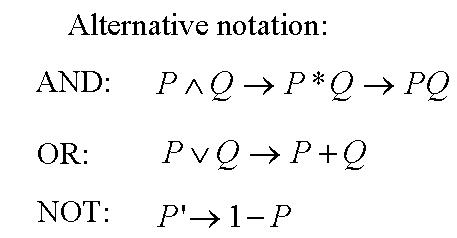
En réalité, il est possible de fabriquer n'importe quoi à l'aide de ces 3 tableaux booléens, donc à partir de AND, OR et NOT. Il existe d'ailleurs une autre porte logique utile, créée à partir des 3 précédentes, la porte XOR.
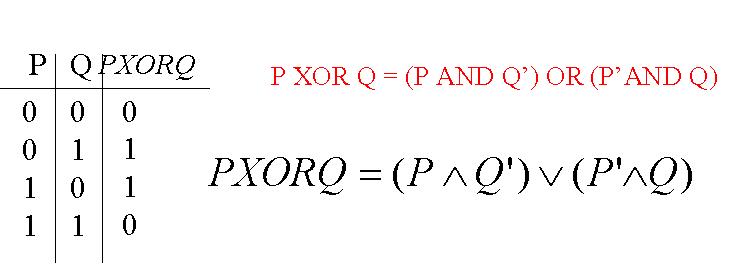
En fait, à l'aide des deux seuls AND et NOT, il est également possible de générer n'importe quoi. Mais on peut aller encore plus loin. Les AND et NOT peuvent créer une cinquième porte NAND qui à elle seule permet de créer n'importe quoi.
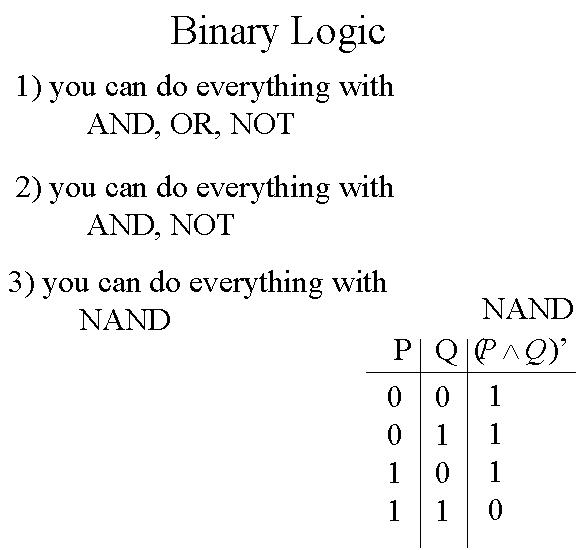
Voici comment on peut à partir d'une porte NAND retrouver les portes AND, OR et NOT.
mettez Q=1 dans P NAND Q --> (P^Q)' --> (P^1)' --> P' --> NOT P mettez Q2=1 dans (P NAND Q1) NAND Q2 --> ((P^Q1)' ^ Q2)' --> ((P^Q1)' ^ 1)' --> ((P^Q1)')' --> P^Q1 --> P AND Q1 NOT P NAND NOT Q --> (P'^Q')' --> PvQ --> P OR Q
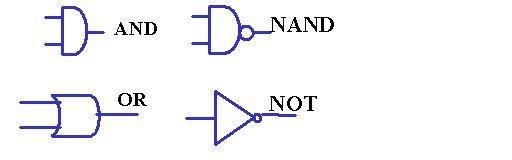
On peut représenter les portes logiques à l'aide de schémas afin de dessiner les circuits en question. Nous allons maintenant construire diverses structures à l'aide de ces portes logiques.
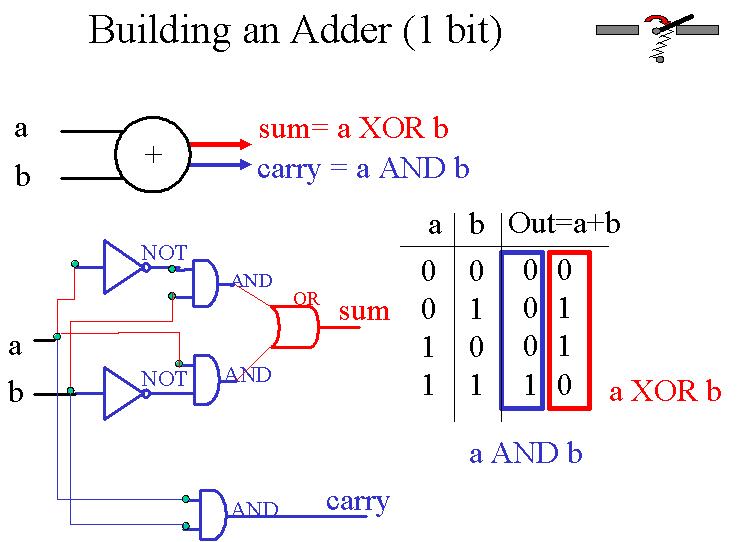
Voici comment on construit un additionneur binaire.
On commence par créer un 1-bit adder. Un 1-bit adder est tout d'abord
constitué d'une sous-unité appelée un half adder. Le half
adder possède deux entrées, une pour chaque bit à additionner. Si les deux bits
sont 1, il nous faut garder en mémoire une retenue qui sera reportée plus tard, alors que la somme en question vaut 0. Si un des deux bits
est 1, l'autre 0, il n'y a pas de retenue et la somme doit valoir 1. Si les deux bits sont 0, alors la somme et la retenue sont toutes
deux nulles. Ceci est possible, une porte XOR schématisant la somme, une porte AND la retenue.
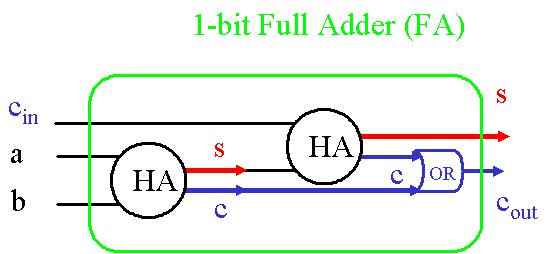
Implémentons maintenant ce half adder dans une structure plus complexe pour obtenir un 1-bit adder, soit un full adder.
Pour terminer, voici comment construire un multi-bit adder. Chaque carry-out d'un FA sert de carry-in pour le FA suivant. C'est une architecture "en cascade".
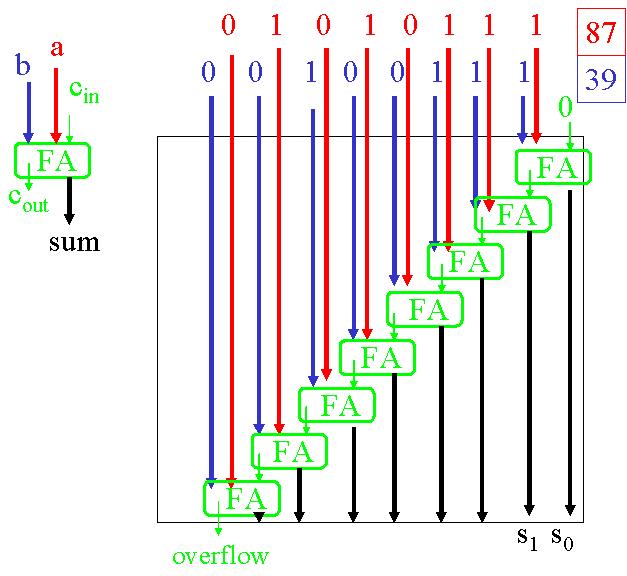
On peut aisément effectuer des opérations élémentaires sur les chiffres binaires. Exercez-vous à additionner, multiplier et soustraire de tels chiffres (avec les astuces vues dans les séries).
Nous allons maintenant construire un multiplexeur. Un multiplexeur est une porte capable de switcher entre différents
chemins, différentes opérations. C'est sur ce principe qu'est basé le "Arithmetic and Logic Unit" (ALU) de notre ordinateur PIPPIN, porte qui doit pouvoir
faire la distinction entre 8 commandes différentes (ADD, MUL, SUB, DIV, AND, NOT, CPL, CPZ).
Commençons
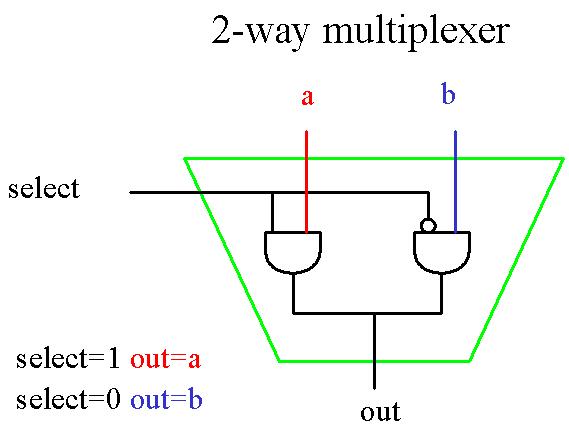
par construire un 2-way multiplexer qui permet de choisir entre deux opérations.
Si SELECT = 1, la sortie est donnée par a. Si SELECT = 0, la sortie est dictée
par b.
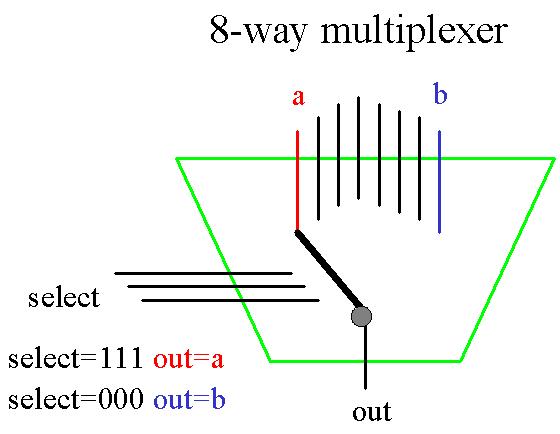
A partir de ce même principe, nous pouvons construire un 8-way multiplexer. Cette fois-ci, il nous faut 3 bits SELECT, dont les 23 différentes combinaisons possibles permettent de distinguer les 8 différentes commandes possibles. Il peut être représenté par 7 multiplexeurs 2-way en série (voir série 3).
En général, pour n entrées, il faut employer log(n) bits SELECT. Aussi, un multiplexeur à n entrées (n étant une puissance de 2) peut être représentée par (n-1) multiplexeurs à 2 entrées.
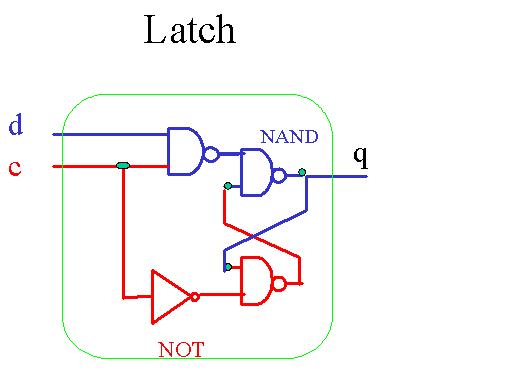
Toute donnée est stockée en mémoire, plus précisément dans les diverses cellules de la mémoire. Pour comprendre le principe d'une mémoire, il nous faut donc tout d'abord construire une cellule simple. Une telle cellule est constituée d'une entité plus simple encore appelée latch. Voici comment implémenter un latch. d est une donnée, c est un signal de contrôle, q est une sortie. Lorsque c=0, quel que soit d, q=0, donc rien ne se passe. Lorsque c=1, quel que soit d, q=d, donc on met d dans q.
Insérons ensuite ce latch dans une 1-bit memory.
Lorsque SELECT = 0,
quel que soit WRITE, c=0 et comme vu précédemment, rien ne se passe. Lorsque
SELECT = 1, si WRITE = 0, c=0 et DATA est en lecture. Si par contre SELECT = 1 et
WRITE = 1, c=1 et DATA est stocké en mémoire. Donc, SELECT nous donne la possibilité de séléctionner ou non la cellule. WRITE nous permet de dicter si nous voulons lire ou écrire une donnée, charger ou stocker
une donnée. DATA contient la donnée à traiter.
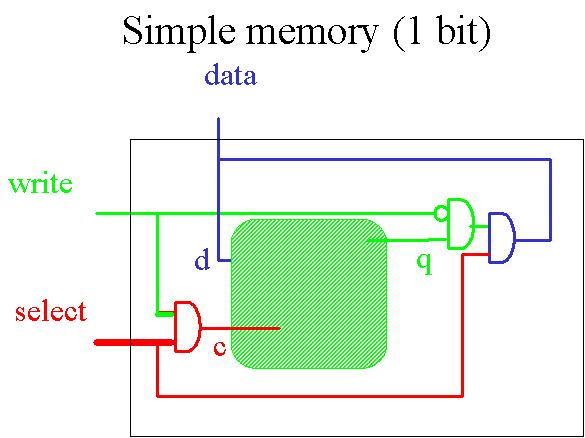
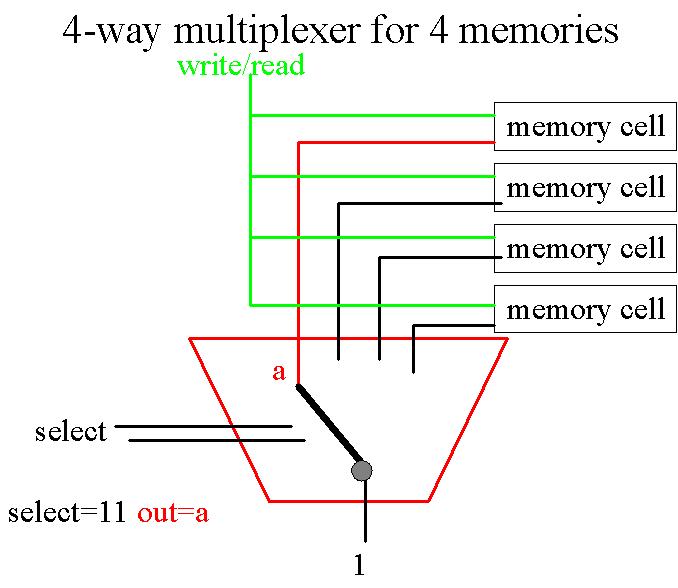
Voyons plus précisément à quoi sert le SELECT. SELECT nous permet de distinguer les 2 situations suivantes. Lorsque SELECT = X et WRITE = 0, la valeur stocké en cellule X est chargée, ce qui correspond à notre commande PIPPIN LOD X. Lorsque SELECT = X et WRITE = 1, la valeur est stockée en mémoire à l'addresse X, ce qui correspond à la commande STO X.
Enfin il faut savoir distinguer entre la commande LOD N et la commande LOD #N. En fait, ce sont deux commandes différentes. Alors pour que PIPPIN sache faire cette distinction, le code binaire de la commande LOD est different de celui de la commande LOD#. La distinction se fait par un bit additionel.

Après avoir vu comment fonctionne une 1-bit memory, voici comment implémenter une 8-bit memory.
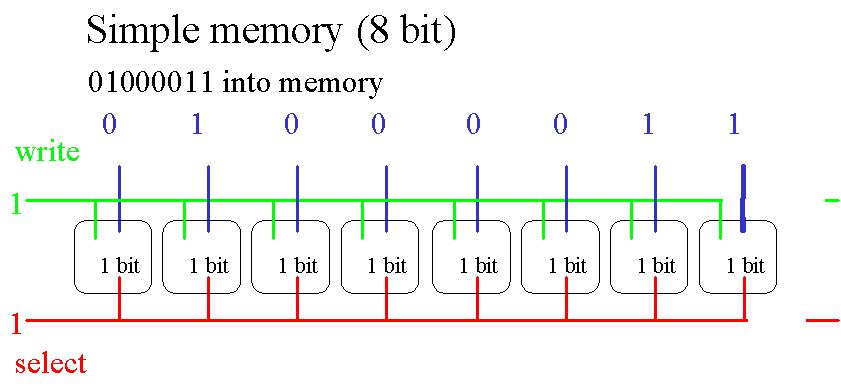
On peut enfin associer multiplexer et mémoire.