Partie II - Qu'est-ce que le calcul? ?

Machine de Turing

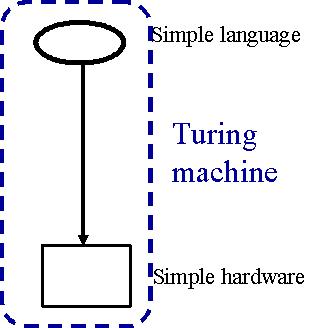
Dans ce chapitre, nous allons implémenter une machine, un ordinateur simplifié qui nous permettra par une procédure pas à pas (un algorithme), de résoudre certains problèmes ou de réaliser certaines tâches. Cette machine se nomme "Machine de Turing" (MdT par la suite). Tous les ordinateurs, aussi complexes soient-ils, peuvent être ramenés à une MdT. La MdT est donc un modèle très puissant.

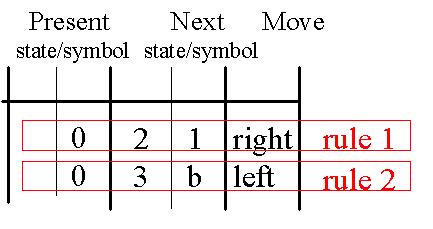
Une machine de Turing est composée d'une bande sur laquelle sont inscrits un certain nombre de symboles, d'une tête de lecture/écriture qui permet de lire, d'écrire ou d'effacer les caractères, et d'un nombre fini de règles qui dictent à la machine son comportement. Chaque règle doit traîter des points suivants  (dans l'ordre):

• 1: Vérifier dans quel état la machine se trouve actuellement (par exemple : état 1, 4, STOP, etc.)
• 2: Lire le présent symbole sur la bande (par ex. : 0, 1, b, etc.)
• 3: Donner l'état futur de la machine (qui peut être le même que l'état actuel).
• 4: En fonction de l'état interne actuel (point 1) et du symbole lu (point 2), effectuer une tâche précise (par ex effacer le symbole actuel, remplacer le présent symbole, etc.)
• 5: Se déplacer sur la bande vers la droite ou vers la gauche

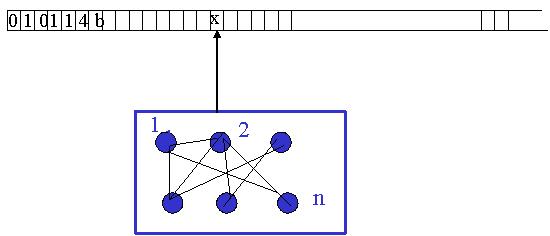
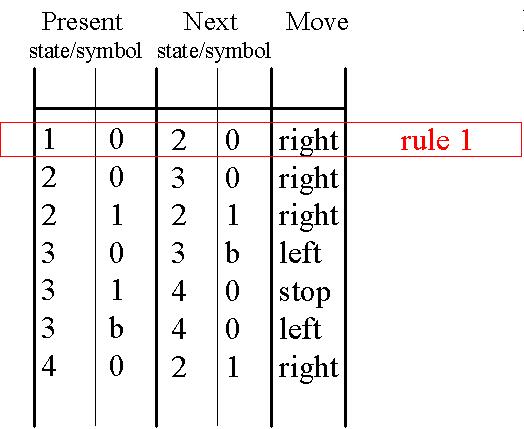
On peut regrouper les règles d'une machine de Turing dans un tableau et les coder à l'aide des codes binaires suivants :

Début/fin de tableau              --> 111
Séparation entre deux règles      --> 11
Séparation entre deux colonnes    --> 1
Etats internes                    --> n fois 0 pour l'état interne n
Symboles            0         --> 0
                    1         --> 00
                    b (blanc) --> 000
Déplacement         à gauche     --> 0
                    à droite     --> 00

Machine à états finis

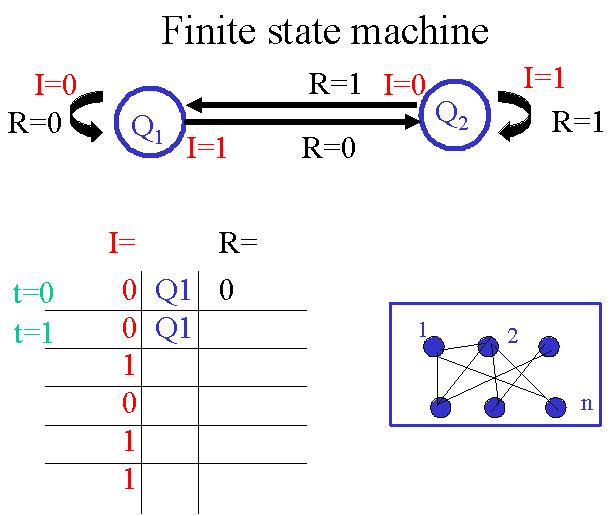
Comme mentionné ci-dessus, une machine de Turing doit présenter un nombre fini de règles, donc également un nombre fini d'états. C'est pourquoi on les appelle machines à états finis. Plus précisement, une Machine à états finis est comme une machine de Turing, mais sans le ruban illimité. Il existe une façon particulière de représenter de telles machines. Chaque état est représenté par un cercle Q(t). Les transitions entre les différents états sont représentées par des flèches reliant les états en question. Le symbole "en lecture" I(t) est noté proche de la queue de la flèche, le symbole "en écriture" R(t) est noté proche de la pointe de la flèche.
Les symboles "en écriture" et la succession d'états sont des fonctions de Q(t) et I(t).

• R(t) = F (Q(t), I(t))
• Q(t+1) = G (Q(t), I(t))

Machine de Turing universelle U

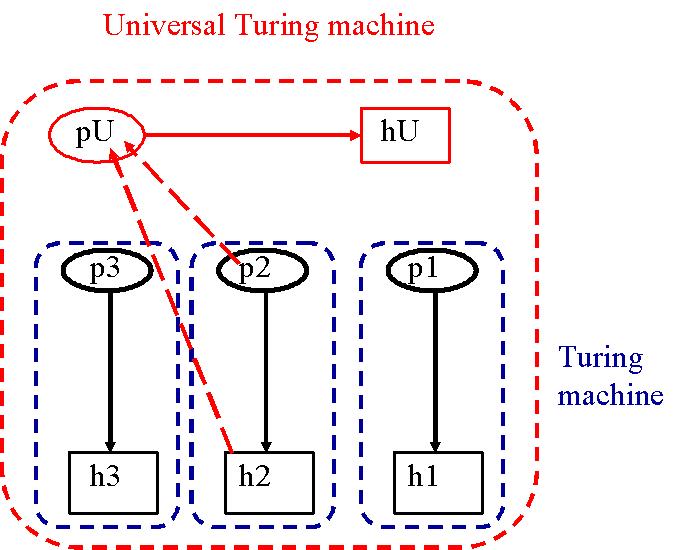
Nous souhaitons construire une machine de Turing universelle U qui puisse à elle seule résoudre un certain nombre i de problèmes intéressants.
La première étape pour construire une telle machine consiste à créer individuellement toutes les machines de Turing t_1...i capables de résoudre les problèmes d'intérêt en question et d'écrire leurs règles sur la bande de la machine de Turing universelle.

• Lire et mémoriser l'état courant et le symbole de t₁
• Aller chercher la règle appropriée de t₁ sur la bande de U
• Mémoriser le nouvel état et la tâche à accomplir correspondant à la règle de t₁
• Effectuer la tâche en question sur la bande de U
• Déplacer le marqueur M sur la bande de U

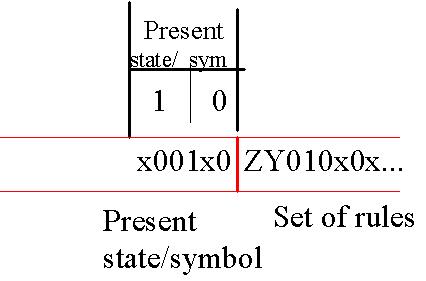
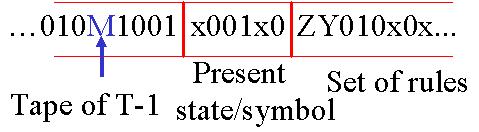
Position de la tête de lecture --> M
Début de la bande de U              --> S
Début/fin de tableau                --> Z
Séparation entre deux règles        --> Y
Séparation entre deux colonnes      --> x
Etats internes                      --> équivalent binaire de l'état (000: "0", 111: "7")
Symboles            0         --> 0
                    1         --> 1
                    b (blanc) --> b
Déplacement         à gauche  --> 0
                    à droite  --> 1

Algorithmes

Quel que soit le langage de programmation utilisé, le raisonnement algorithmique est à la base de tout programme. Toute question, tout problème, problème de décision, problème arithmétique ou autre, doit être abordé de façon systématique et rigoureuse, suivant une démarche reproductible. Une telle procédure pas à pas s'appelle un algorithme.

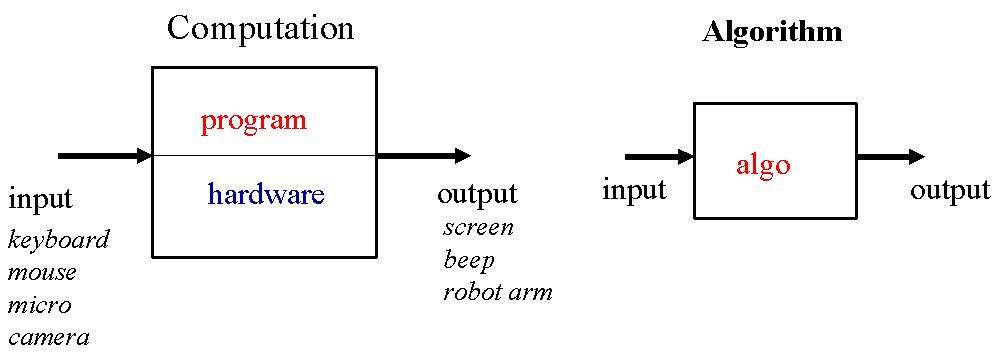
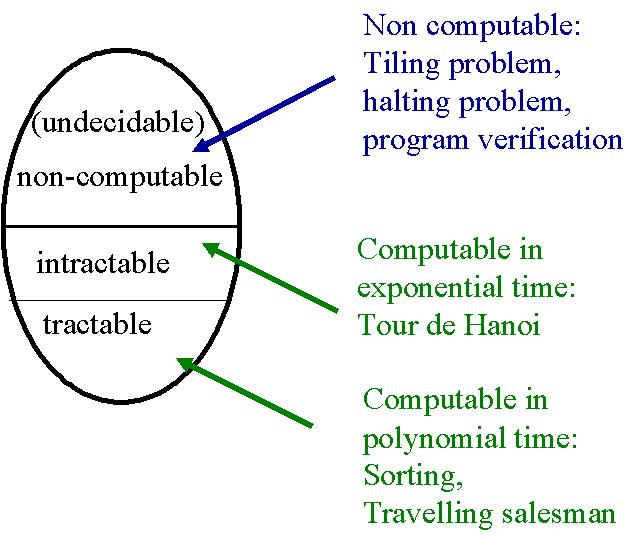
Il existe différentes sortes de problèmes. En voici quelques exemples :

• Problème arithmétique : Trouver le plus grand diviseur commun entre deux nombres, dire si un nombre est premier ou non, etc.
• Problème non arithmétiques : Dire si l'on peut couvrir une surface donnée à l'aide d'un nombre donné de carreaux (tiling problem), etc.
• Problème de décision : Dire si un programme s'interrompt ou non (halting problem), etc.

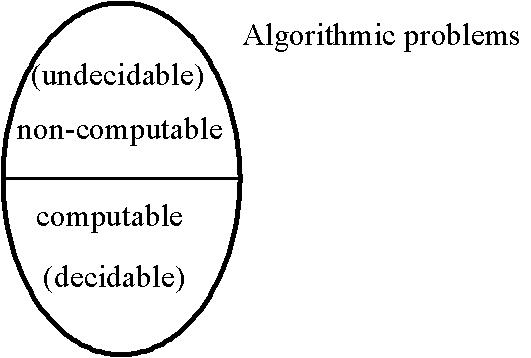
Voici des exemples de problèmes non résolvables : Tiling problem, halting problem.

Problème de l'arrêt

Le problème de l'arrêt ("Halting Problem" en anglais, on l'appelera par la suite HP) pose la question suivante : Existe-t-il un algorithme qui, appliqué à un programme informatique dont le but est de résoudre un problème quelconque, est capable de dire si oui ou non ce programme va s'arrêter. Voici deux exemples de boucles òu c'est facile (boucle 1) ou difficile (boucle 2) de voir si elles s'arrêten.

Boucle 1                Boucle 2
{                    {
while (n != 1)                while (n != 1)
    n = n-2;                {
return n;                    if (n%2 == 0)
}                            n = n/2;
                        else
                            n = 3*n+1;
                        }   
                    return n;
                    }

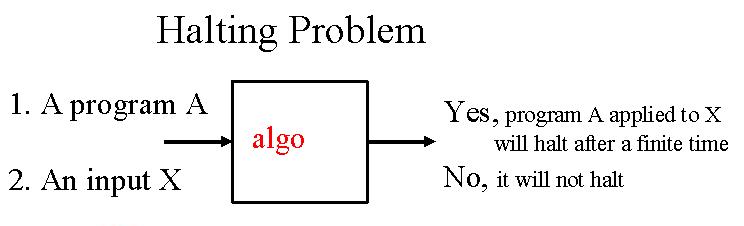
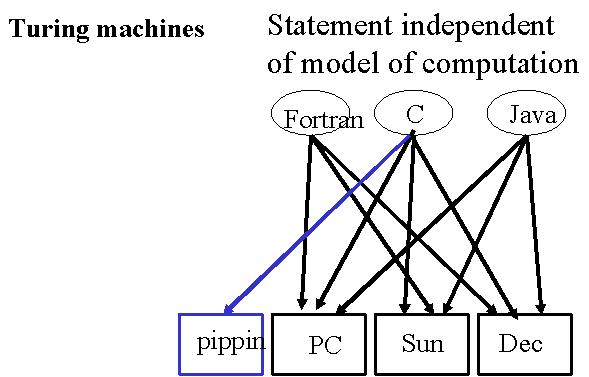
La première étape de la démonstration consiste à faire l'hypothèse qu'un programme arbitraire corresponds à une machine de Turing. Or on peut démontrer que l'on peut établir une liste de TOUTES des machines de Turing alors de TOUS les programmes possibles et imaginables et les utiliser comme première entrée d'un tableau à deux dimensions.
La deuxième étape consiste à démontrer l'hypothèse que l'on peut également imaginer et anticiper toutes les entrées possibles et imaginables à un problème et les utiliser comme autre entrée de notre tableau à double entrée.

Nous faisons maitenant l'hypothèse qu'un algorithm HP existe. Dans notre tableau, nous pouvons donc voir si une entrée appliquée à un programme s'arrête ou non.

Raisonnons ensuite par l'absurde et imaginons un programme inverse N, qui ait pour fonction de renvoyer un "oui" si le programme ne s'arrête pas, un "non" si le programme s'arrête.
Ceci implique que le comportement de N est différent des comportements des programmes (1, 2, 3, etc) pour au moins une entrée. Un tel programme n'apparaît donc évidemment pas dans notre tableau et nous donne les réponses inverses à celle renvoyées sur la diagonale de notre tableau. Seulement, étant donné que notre liste est prétendument complète, alors on a une contradiction.
En raisonnant par l'absurde, on voit qu'il est donc tout simplement impossible de trouver un algorithme qui permette de résoudre HP.

Ordres de complexité

Revenons maintenant aux problèmes résolvables. Un algorithme, pour résoudre un problème, nécessite un certain temps de "processing" qui est proportionnel au nombre d'exécutions que l'algorithme doit effectuer. Prenons l'exemple d'un algorithme qui fait la somme des salaires des N employés d'une entreprise. Pour faire cette somme, l'algorithme doit passer en revue tous les salaires et les additionner. Le nombre d'étapes est donc N, quel que soit le nombre d'employés. On parle de l'ordre de complexité d'un algorithme et on écrit O (N).

Lorsque l'on détermine l'ordre de complexité d'un algorithme, les fonctions exponentielle de N écrasent les fonctions polynomiales de N, qui écrasent les fonctions logarithmiques de N. Donc, lorsque l'on donne cet ordre de complexité, on ne garde que le terme prépondérant.

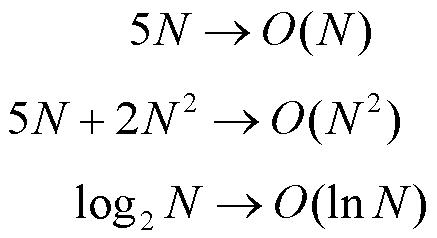
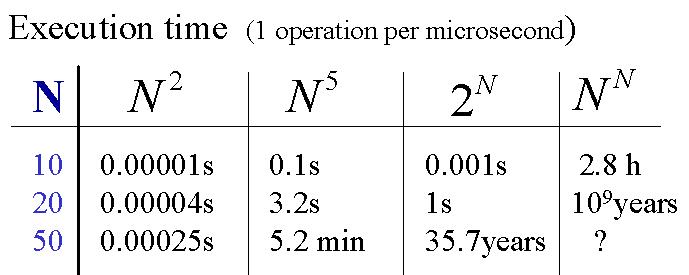
Afin d'illustrer les ordres de complexité, nous allons étudier deux différents algorithmes de tri de nombres et comparer leur ordres de complexité. Familiarisez-vous avec ces deux algorithmes.

• Tri par bulle : ordre de complexité O (N²).
• Tri par fusion : ordre de complexité O (N ln N).

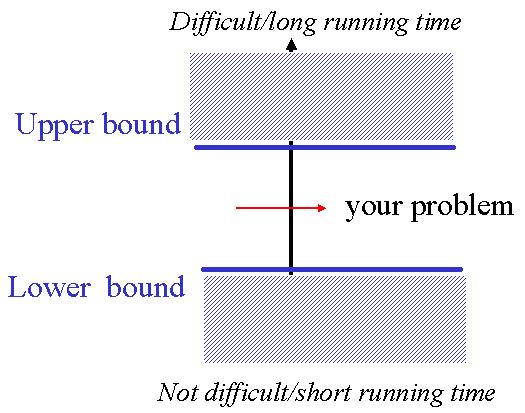
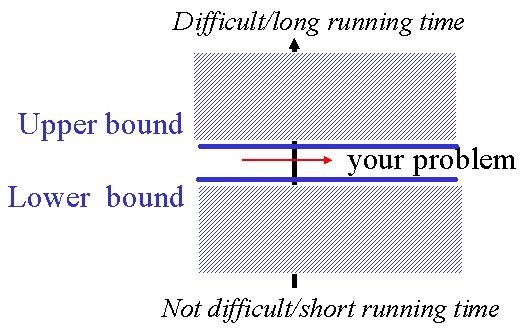
Comment est-ce qu'on peut savoir si un algorithme est `bon'? Pour certains problèmes les experts de maths ou de l'informatique théorique ont pu démontrer qu'un algorithme arbitraire doit de toute manière faire un nombre minimal de pas. Par exemple, pour sommer une liste, on doit de toute manière toucher chaque élément de la liste au moins un fois. Ce type de raisonnement peut alors donner une borne inférieure pour le meilleur algorithme sans spécifier un algorithme particulier. En même temps, si on a un algorithme donné, on peut determiner sa complexité ce qui donne une borne supérieure pour la solution du problème algorithmique. Souvent il existe un écart entre l'efficacité du meilleur algorithme connu (borne supérieure) et la borne inférieure. Plus l'écart est grand, plus cela vaut la peine de chercher un meilleur algorithme. Dans le cas idéal, notre alorithme a une complexité qui conincide avec celle de l'algorithme optimal (Lower Bound).

• Problèmes pour lesquels la tranche est minuscule : Tour de Hanoi
• Problèmes pour lesquels la tranche est petite : Dire si un nombre est premier ou non, tri
• Problèmes pour lesquels la tranche est grande : Travelling salesman

Programmation dynamique - algorithme de Needleman-Wunsch

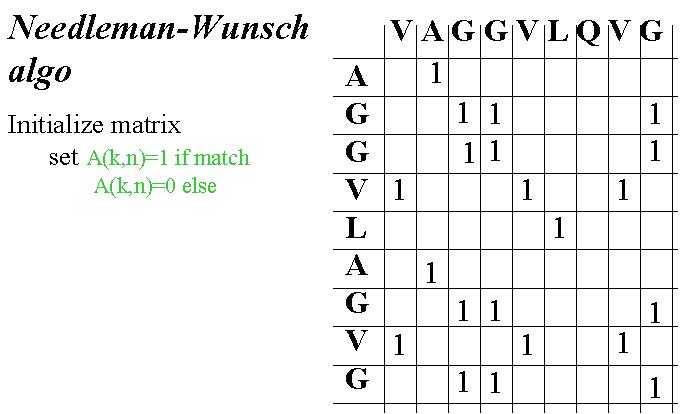
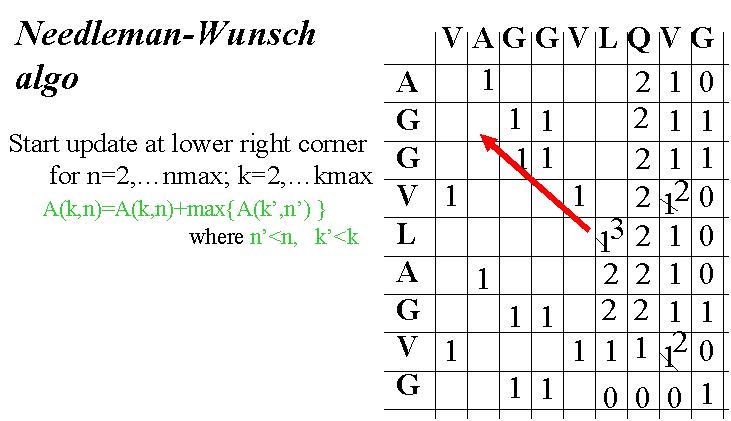
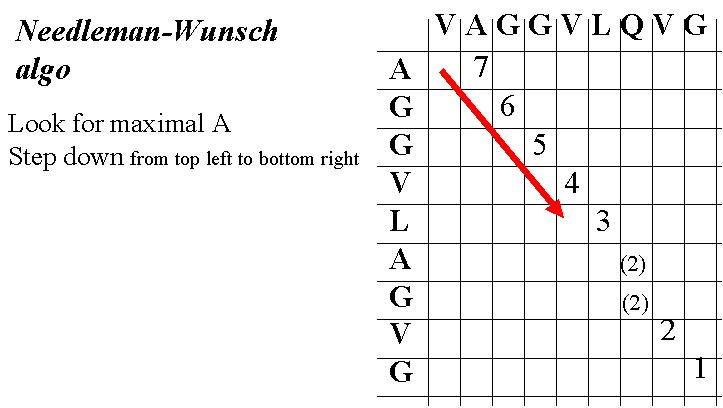
La programmation dynamique, en s'appuyant sur des algorithmes, permet de résoudre des problèmes par une procédure pas à pas exhaustive. Un exemple d'application de la programmation dynamique est la recherche d'alignement optimal de gènes. Elle s'appuye sur trois idées :

• Maximiser l'alignement d'une séquence --> Max { A(N,K) } où N et K sont les longueurs respectives des deux séquences à aligner
• Subdiviser l'alignement de séquences --> A(N,K) = 1 + Max { A(N-1,K-1) } si il y a une correspondance dans la position N et K.
• Employer une matrice pour trouver l'alignement optimal

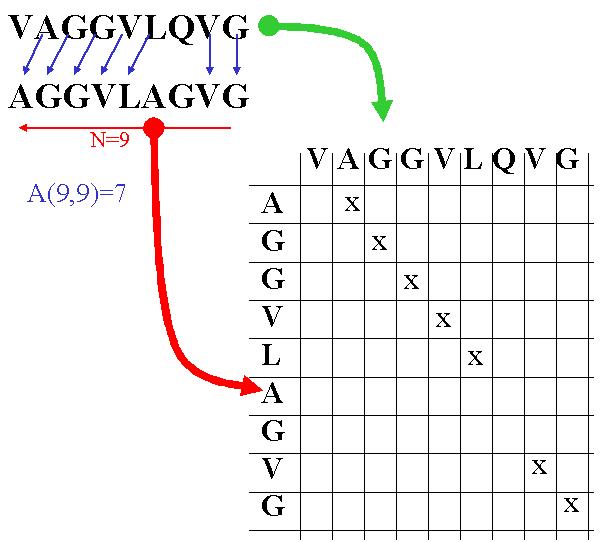
L'algorithme de Needleman-Wunsch est un algorithme efficace pour l'alignement de séquences. Il suit les trois étapes suivantes :