Partie III - Qu'est-ce que l'information? 

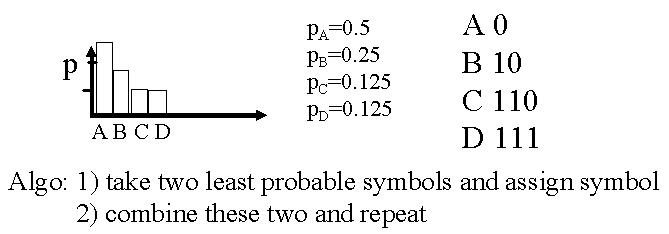
Peut-on quantifier le contenu d'une information à transmettre ? Combien d'information est perdue lors d'une transmission ? Comment peut-on minimiser cette perte ? Jusqu'à quel point peut-on compresser un document sans perdre d'information ? Voici le genre de questions auxquelles tente de répondre la théorie de l'information.

Codes de correction d'erreur

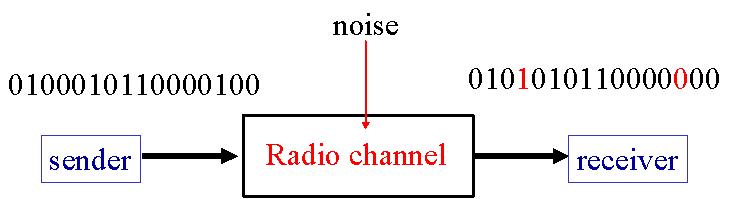
Au cours de la transmission d'un document au travers d'un canal bruité, il y a toujours une probabilité p pour qu'un bit soit transmis incorrectement. Ce "bit flip" est dû au bruit dans le canal. Le nombre de bits mal transmis sur un message de longueur N est N*p.

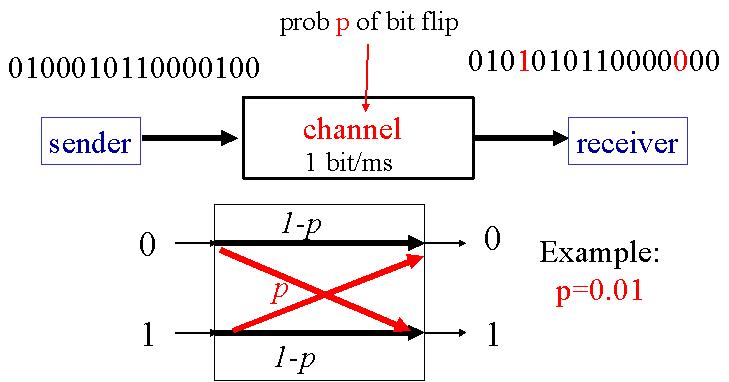
L'information reçue peut donc être sensiblement différente de celle envoyée.

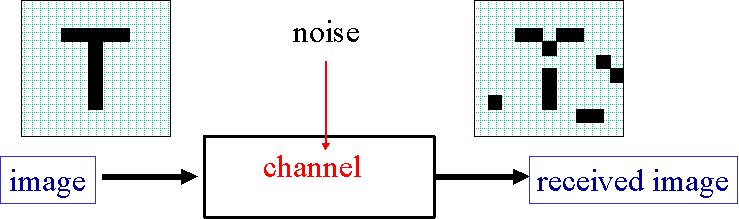
Il existe différents moyens de coder une information afin de récupérer celle-ci intacte après transmission. Nous allons voir quelques-uns de ces codes.

• Codage par répétition
  Le codage par répétition consiste à envoyer chaque bit plusieurs fois, par exemple trois fois plutôt qu'une. Le décodage se fait en renvoyant le bit majoritaire sur les trois bits (principe de votation). Ce code permet donc de coder et d'améliorer la transmission d'une information.

  00010 --> 
  codage --> 
  000 000 000 111 000 --> 
  canal bruité --> 
  001 000 010 110 000 --> 
  décodage --> 
  00010
  

  Mais ce code ne peut pas garantir qu'aucune information ne soit perdue. En effet, si la probabilité de bit flip est importante, les bits peuvent être mal décodés.

  00010 --> 
  codage --> 
  000 000 000 111 000 --> 
  canal bruité --> 
  011 000 011 110 000 --> 
  décodage --> 
  10110
  

  Ce code implique d'envoyer trois fois plus de bits par rapport au message initial. Le taux de transmission est le rapport entre la longueur du message initial et la longueur du message après codage. Un excellent taux de transmission est donc proche de 1. Dans notre cas, le taux de transmission est de 1/3.
  

Pour améliorer la qualité de la transmission de l'information et diminuer le risque de voir un bit mal décodé, on peut envoyer chaque bit cinq fois. La probabilité que les bit flips soient suffisamment nombreux pour qu'un bit soit mal décodé est fortement diminuée. Cette probabilité existe néanmoins. On la calcule ainsi :


Où m est égale la partie entière de N/2, à laquelle on ajoute 1. Par ex., pour N=7, m=¦7/2¦+1 = 3+1 = 4.
Le taux de transmission est alors de 1/5, donc moins favorable que précédemment.
• Parity check code
  Le parity check code consiste à ajouter un ou plusieurs bits de contrôle à la fin du message à envoyer. Commençons par considérer le cas où m=1, c'est-à-dire où un unique bit de contrôle est employé. Pour déterminer le bit de contrôle, il faut compter le nombre de 1 envoyés dans le message initial. Si ce nombre est pair, le bit de contrôle est 1. Si le nombre de 1 est impair, le bit de contrôle est 0.
  

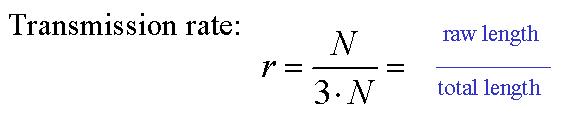
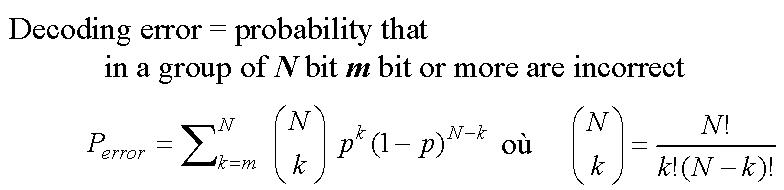
  Le taux de transmission est très proche de 1, donc excellent (ici, m=1).

  

  Cela dit, notre bit de contrôle permet de détecter qu'une erreur est survenue dans la transmission d'un message, mais ne permet pas de localiser et de corriger l'erreur. Il est possible de remédier à ce problème en employant plusieurs bits de contrôle. Prenons par exemple m=3, trois bits de contrôle. On parle d'un code Hamming H(7,4) si l'on emploie trois bits de contrôle pour coder un message initial de quatre bits. Le premier des trois bits de contrôle code pour une combinaison de trois des quatre bits du message initial, le second bit de contrôle code pour une autre combinaison de trois des quatre bits du message initial, le troisième bit de contrôle code pour la troisième combinaison de trois des quatre bits du message initial. Les trois bits de contrôle permettent 2³ = 8 configurations différentes, donc permettent de détecter et localiser une erreur sur un message final de 7 bits.
  Le taux de transmission est de 4/7.

  

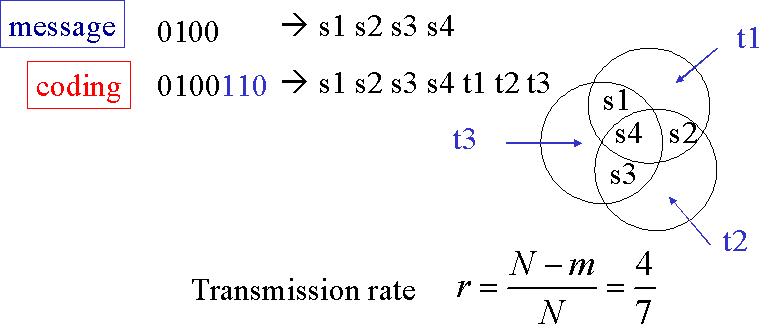
  Par exemple, si seul t1 est faux, alors le bit de parité t1 a été mal reçu, il faut le changer). Par contre, si t1 ET t2 sont faux, alors la cause se situe dans le bit de données commun à t1 et t2 : s2 est faux, il faut donc le changer (le mettre à 1 s'il est à 0, et vice-versa).

  On peut employer ce même code de Hamming avec de plus nombreux bits de contrôle. Voici deux cas à comparer.

  

  Les codes de Hamming permettent de localiser et de corriger une erreur unique. Ils permettent également de localiser et corriger deux erreurs ou plus si le nombre de bits dans le message initial est moins important. Voici comment on procède au calcul :

  

Comparons désormais un code de répétition et deux codes de Hamming.

L'entropie

L'entropie est en quelque sorte l'incertitude existante et appariée à un problème, à une question. Prenons l'exemple d'un chocolat qu'il s'agit de retrouver dans N boîtes fermées et considérons que la probabilité d'être dans chaque boîte est identique.
Si N=1, alors l'entropie est nulle, car on est sûrs de savoir où se trouve le chocolat (pas d'incertitude).
Si N=2, nous avons une chance sur deux de trouver le chocolat du premier coup, on dit que la probabilité de trouver le chocolat est de 1/2. L'incertitude augmente, et l'entropie avec.
Si N=4, une chance sur quatre, la probabilité est alors de 1/4, entropie encore augmentée, etc. L'entropie augmente donc avec N et suit un comportement logarithmique. On note l'entropie H = f(N) = log₂N comme fonction de N.
Dans notre exemple, la probabilité d'être dans chaque boîte était identique, mais il arrive dans de nombreux problèmes que la distribution de probabilité ne soit pas homogène. L'entropie se comporte alors différemment.

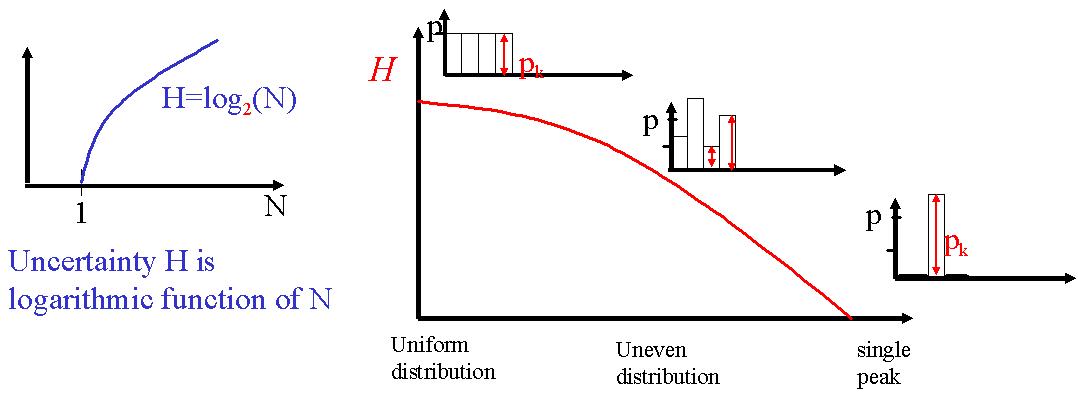
Ici, nous avons 3 cas de figure :
1: une distibution équiprobable. Dans ce cas, l'incertitude est maximale : on ne sait pas à priori dans quelle "boîte" commencer pour trouver le chocolat.
2: une distribution inhomogène : l'incertitude est plus faible, car l'on aura tendance, par exemple, à chercher d'abord dans les boîtes aux probabilités les plus hautes (les 2 plus hautes barres).
3: une distribution sur un pic : l'incertitude est nulle : on a toutes les chances de trouver le chocolat dans la boîte dont la probabilité est 1.

La somme des probabilités liées à un évènement vaut 1, quelle que soit la distribution des probabilités.

L'entropie H est très importante, car elle nous donne de nombreuses informations. Elle nous donne par exemple le nombre minimal de questions qu'il est nécessaire de poser pour répondre à une énigme, une borne inférieure pour la compression d'un document, etc. Prenons l'exemple d'une séquence composée de N différents éléments. Il existe 2^NH séquences significatives et chacune de ces séquences a une probabilité 2^-NH d'apparaître. Les autres séquences n'ont qu'une probabilité négligeable d'apparaître.
Une autre information précieuse est l'information mutuelle I. L'information mutuelle est donnée par la différence entre l'entropie de départ et d'arrivée.

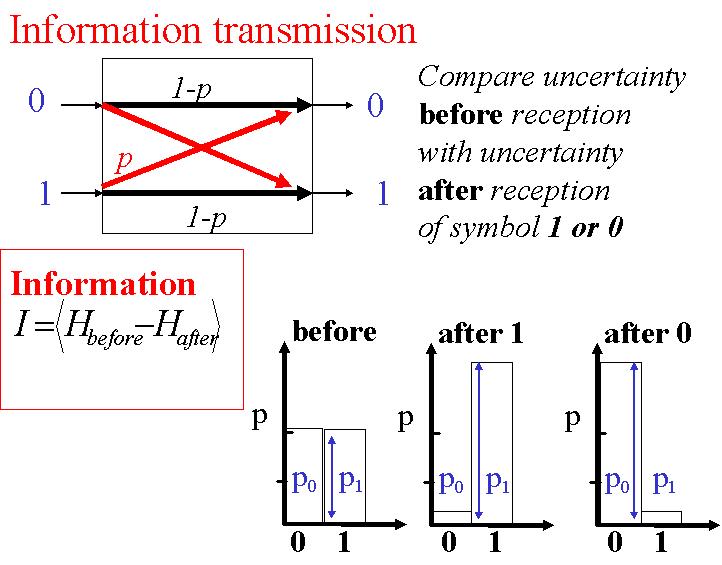
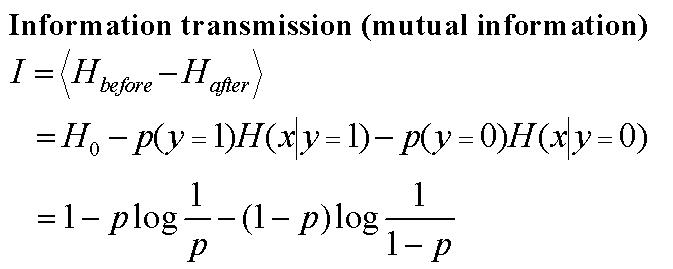
Cette information est à la base de la théoriede Shannon. Celui-ci nous dit qu'une communication fiable peut être effectuée en présence d'un canal bruité et ceci à un taux de transmission fini r pour autant que l'information transmise soit suffisamment importante. Dans ce cas, r=I.

Calcul des probabilités

Le calcul des probabilités est très utile. Familiarisez-vous avec les formules importantes et leur maniement.

Codes de compression

Afin de gagner du temps lors de la transmission d'une information, il est intéressant de pouvoir compresser un document, un texte, une image. L'entropie prend ici toute son importance. Elle nous donne une borne inférieure pour la compression. En effet, la compression d'une séquence de N bits nécessite au moins NH bits à émettre et H est le nombre moyen de bits à émettre. Nous allons voir différents codes de compression.

• Huffmann code
  Ce code se base sur l'idée simple que les symboles à envoyer les plus fréquents doivent être codés avec le moins de bits possibles, alors que les symboles apparaissant moins fréquemment peuvent être codés avec plus de bits. Il suit l'algorithme suivant :
  

• Code prédictif - Lempel ziv
  Ce code de compression de texte s'appuie sur l'idée que les lettres sont corrélées entre elles, qu'elles apparaissent le plus souvent sous forme de blocs et qu'il peut être avantageux de coder ces blocs en plus des lettres individuellement. Il suit l'algorithme suivant :