Neurons in the cortex and other areas of the brain often exhibit
highly developed dendritic trees that may extend over several hundreds
of ![]() m. Synaptic input to a neuron is mostly located on its
dendritic tree, spikes, however, are generated at the soma near the
axon hillock. What are the consequences of the spatial separation of
input and output? Up to now we have discussed point neurons only,
i.e., neurons without any spatial structure. The electrical properties
of point neurons have been described as a capacitor that is charged by
synaptic currents and other transversal ion currents across
the membrane. A non-uniform distribution of the membrane potential on
the dendritic tree and the soma induces additional longitudinal current along the dendrite. We are now going to derive
the cable equation that describes the membrane potential along a
passive dendrite as a function of time and space. In
Section 2.6 we will see how geometric and
electrophysiological properties of a certain type of neuron can be
integrated in a comprehensive biophysical model.
m. Synaptic input to a neuron is mostly located on its
dendritic tree, spikes, however, are generated at the soma near the
axon hillock. What are the consequences of the spatial separation of
input and output? Up to now we have discussed point neurons only,
i.e., neurons without any spatial structure. The electrical properties
of point neurons have been described as a capacitor that is charged by
synaptic currents and other transversal ion currents across
the membrane. A non-uniform distribution of the membrane potential on
the dendritic tree and the soma induces additional longitudinal current along the dendrite. We are now going to derive
the cable equation that describes the membrane potential along a
passive dendrite as a function of time and space. In
Section 2.6 we will see how geometric and
electrophysiological properties of a certain type of neuron can be
integrated in a comprehensive biophysical model.
![\centerline{\includegraphics[width=6cm]{cable_equation.ps.gz}}](img181.gif) |
Consider a piece of a dendrite decomposed in short cylindric segments of length dx each. The schematic drawing in Fig. 2.16 shows the corresponding circuit diagram. Using Kirchhoff's laws we find equations that relate the voltage u(x) across the membrane at location x with longitudinal and transversal currents. First, a longitudinal current i(x) passing through the dendrite causes a voltage drop across the longitudinal resistor RL according to Ohm's law,
| RL = rL dx , R-1T = r-1T dx , C = c dx , Iext(t, x) = iext(t, x) dx . | (2.25) |
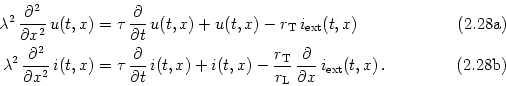 |
| x |
(2.29) |
| i |
(2.30) |
The cable equations can be easily interpreted. These equations describe the change in time of voltage and longitudinal current. Both equations contain three different contributions. The first term on the right-hand side of Eq. (2.32) is a diffusion term that is positive if the voltage (or current) is a convex function of x. The voltage at x thus tends to decrease, if the values of u are lower in a neighborhood of x than at x itself. The second term on the right-hand side of Eq. (2.32) is a simple decay term that causes the voltage to decay exponentially towards zero. The third term, finally, is a source term that acts as an inhomogeneity in the otherwise autonomous differential equation. This source can be due to an externally applied current, to synaptic input, or to other (non-linear) ion channels; cf.Section 2.5.3.
In order to get an intuitive understanding of the behavior of the
cable equation we look for stationary solutions of Eq. (2.32a), i.e., for solutions with
![]() u(t, x)/
u(t, x)/![]() t = 0. In that
case, the partial differential equation reduces to an ordinary
differential equation in x, viz.
t = 0. In that
case, the partial differential equation reduces to an ordinary
differential equation in x, viz.
| (2.32) |
| u(t, x) = c1 sinh(x) + c2 cosh(x) , | (2.33) |
Solutions for non-vanishing input current can be found by standard
techniques. For a stationary input current
iext(t, x) = ![]() (x)
localized at x = 0 and boundary conditions
u(±
(x)
localized at x = 0 and boundary conditions
u(±![]() ) = 0 we find
) = 0 we find
![\centerline{\includegraphics[width=7cm]{stat_solution.ps.gz}}](img209.gif) |
For arbitrary stationary input current iext(x) the solution of Eq. (2.32a) can be found by a superposition of translated fundamental solutions (2.35), viz.,
| u(t, x) = |
(2.35) |
In the following we will concentrate on the equation for the voltage
and start our analysis by deriving the Green's function for a cable
extending to infinity in both directions. The Green's function is
defined as the solution of a linear equation such as Eq. (2.32) with a Dirac ![]() -pulse as its input. It can be seen as
an elementary solution of the differential equation because - due to
linearity - the solution for any given input can be constructed
as a superposition of these Green's functions.
-pulse as its input. It can be seen as
an elementary solution of the differential equation because - due to
linearity - the solution for any given input can be constructed
as a superposition of these Green's functions.
In order to find the Green's function for the cable equation we thus
have to solve Eq. (2.32a) with
iext(t, x)
replaced by a ![]() impulse at x = 0 and t = 0,
impulse at x = 0 and t = 0,
| (2.37) |
| u(t, k) = exp |
(2.38) |
We can check the validity of Eq. (2.40) by substituting
G![]() (t, x) into the left-hand side of Eq. (2.37). After a
short calculation we find
(t, x) into the left-hand side of Eq. (2.37). After a
short calculation we find
| (2.42) |
Having established that
| (2.43) |
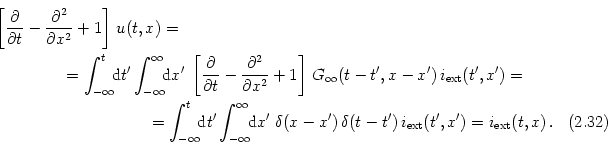
Real cables do not extend from - ![]() to +
to + ![]() and we have to
take extra care to correctly include boundary conditions at the ends.
We consider a finite cable extending from x = 0 to x = L with sealed
ends, i.e.,
i(t, x = 0) = i(t, x = L) = 0 or, equivalently,
and we have to
take extra care to correctly include boundary conditions at the ends.
We consider a finite cable extending from x = 0 to x = L with sealed
ends, i.e.,
i(t, x = 0) = i(t, x = L) = 0 or, equivalently,
![]() u(t, x = 0) =
u(t, x = 0) = ![]() u(t, x = L) = 0.
u(t, x = L) = 0.
The Green's function G0, L for a cable with sealed ends can be
constructed from G![]() by applying a trick from electro-statics
called ``mirror charges'' (Jackson, 1962). Similar techniques can also
be applied to treat branching points in a dendritic tree
(Abbott, 1991). The cable equation is linear and, therefore, a
superposition of two solutions is also a solution. Consider a
by applying a trick from electro-statics
called ``mirror charges'' (Jackson, 1962). Similar techniques can also
be applied to treat branching points in a dendritic tree
(Abbott, 1991). The cable equation is linear and, therefore, a
superposition of two solutions is also a solution. Consider a ![]() current pulse at time t0 and position x0 somewhere along the
cable. The boundary condition
current pulse at time t0 and position x0 somewhere along the
cable. The boundary condition
![]() u(t, x = 0) = 0 can be satisfied if we add a second, virtual
current pulse at a position x = - x0 outside the interval
[0, L]. Adding a current pulse outside the interval [0, L] comes for
free since the result is still a solution of the cable equation on
that interval. Similarly, we can fulfill the boundary condition at
x = L by adding a mirror pulse at
x = 2 L - x0. In order to account
for both boundary conditions simultaneously, we have to compensate for
the mirror pulse at - x0 by adding another mirror pulse at
2 L + x0 and for the mirror pulse at
x = 2 L - x0 by adding a fourth
pulse at -2 L + x0 and so forth. Altogether we have
u(t, x = 0) = 0 can be satisfied if we add a second, virtual
current pulse at a position x = - x0 outside the interval
[0, L]. Adding a current pulse outside the interval [0, L] comes for
free since the result is still a solution of the cable equation on
that interval. Similarly, we can fulfill the boundary condition at
x = L by adding a mirror pulse at
x = 2 L - x0. In order to account
for both boundary conditions simultaneously, we have to compensate for
the mirror pulse at - x0 by adding another mirror pulse at
2 L + x0 and for the mirror pulse at
x = 2 L - x0 by adding a fourth
pulse at -2 L + x0 and so forth. Altogether we have
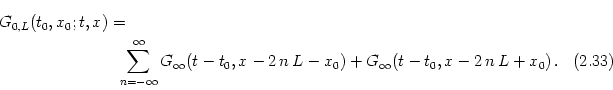
| u(t, x) = |
(2.44) |
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\centerline{\includegraphics[width...
...rline{\includegraphics[width=\textwidth]{voltage_traces_t.ps.gz}} \end{minipage}](img237.gif) |
In the context of a realistic modeling of `biological' neurons two non-linear extensions of the cable equation have to be discussed. The obvious one is the inclusion of non-linear elements in the circuit diagram of Fig. 2.16 that account for specialized ion channels. As we have seen in the Hodgkin-Huxley model, ion channels can exhibit a complex dynamics that is in itself governed by a system of (ordinary) differential equations. The current through one of these channels is thus not simply a (non-linear) function of the actual value of the membrane potential but may also depend on the time course of the membrane potential in the past. Using the symbolic notation iion[u](t, x) for this functional dependence the extended cable equation takes the form
| (2.45) |
A more subtle complication arises from the fact that a synapse can not be treated as an ideal current source. The effect of an incoming action potential is the opening of ion channels. The resulting current is proportional to the difference of the membrane potential and the corresponding ionic reversal potential. Hence, a time-dependent conductivity as in Eq. (2.19) provides a more realistic description of synaptic input than an ideal current source with a fixed time course.
If we replace in Eq. (2.32a) the external input current iext(t, x) by an appropriate synaptic input current - isyn(t, x) = - gsyn(t, x)[u(t, x) - Esyn] with gsyn being the synaptic conductivity and Esyn the corresponding reversal potential, we obtain2.2
| (2.46) |
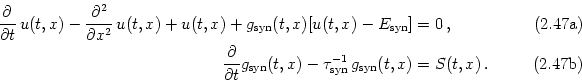 |
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.