... AMPA-receptors^2.1

AMPA is short for 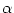$\alpha$-amino-3-hydroxy-5-methyl-4-isoxalone propionic acid.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... obtain^2.2

We want outward currents to be positive, hence the change in the sign of i_ext and i_syn.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... normally^3.1

Exceptions are the rare cases where the function F or G is degenerate; e.g., F(u, w) = w².

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... potential^4.1

Note that in Eq. (4.20) we consider the synaptic current as an external current whereas in Chapter 2 we have considered it as a membrane current and therefore used a different sign convention. In both cases, an excitatory input increases the membrane potential.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... currents^5.1

We neglect here intrinsically bursting and chaotic neurons.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... independent^6.1

In a simulation, spike arrival could for example be simulated by independent Poisson processes

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... past^6.2

Neurons which have never fired before are assigned a formal firing time $\hat{{t}}$ = - $\infty$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

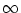... noise^7.1

It is called white noise because the power spectrum (i.e. the Fourier transform of the autocorrelation) is flat. A Poisson process is an example of a statistical process with autocorrelation (7.73); cf. Chapter 5.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... out^9.1

The decay of the activity is exponential in n if 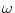$\omega$ < 1; for 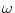$\omega$ = 1 the decay is polynomial in n.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... parameters^9.2

We use a tilde in order to identify parameters that describe the time course of the membrane potential. Parameters without a tilde refer to the firing-time distribution.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... analogously^10.1

Note that w_ij is a step function of time with discontinuities whenever a presynaptic spike arrives or a postsynaptic action potential is triggered. In order to obtain a well-defined differential equation we specify that the amplitude of the step depends on the value of w_ij immediately before the spike. In mathematical terms, we impose the condition that w_ij(t) is continuous from left, i.e., that 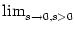$\lim_{{s\to 0, s>0}}^{}$w_ij(t^(f) - s) = w_ij(t^(f)).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Aristoteles^10.2

Aristoteles, "De memoria et reminiscentia": There is no need to consider how we remember what is distant, but only what is neighboring, for clearly the method is the same. For the changes follow each other by habit, one after another. And thus, whenever someone wishes to recollect he will do the following: He will seek to get a starting point for a change after which will be the change in question.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.