




Next: 4.2 Spike response model
Up: 4. Formal Spiking Neuron
Previous: 4. Formal Spiking Neuron
Subsections
4.1 Integrate-and-fire model
In this section, we give an overview of integrate-and-fire models. The leaky
integrate-and-fire neuron introduced in Section 4.1.1 is
probably the best-known example of a formal spiking neuron model.
Generalizations of the leaky integrate-and-fire model include the nonlinear
integrate-and-fire model that is discussed in
Section 4.1.2. All integrate-and-fire neurons can either
be stimulated by external current or by synaptic input from presynaptic
neurons. Standard formulations of synaptic input are given in
Section 4.1.3.
4.1.1 Leaky Integrate-and-Fire Model
Figure 4.1:
Schematic diagram of the integrate-and-fire model. The basic circuit is the
module inside the dashed circle on the right-hand side. A current I(t)
charges the RC circuit. The voltage u(t) across the capacitance
(points) is compared to a threshold  . If
u(t) =
. If
u(t) =  at
time ti(f) an output pulse
at
time ti(f) an output pulse
 (t - ti(f)) is generated. Left part: A
presynaptic spike
(t - ti(f)) is generated. Left part: A
presynaptic spike
 (t - tj(f)) is low-pass filtered at the synapse and
generates an input current pulse
(t - tj(f)) is low-pass filtered at the synapse and
generates an input current pulse
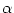 (t - tj(f)).
(t - tj(f)).
![\centerline{ \includegraphics[width=100mm]{I-Fnew.eps}}](img378.gif) |
The basic circuit of an integrate-and-fire model consists of a capacitor C
in parallel with a resistor R driven by a current I(t); see Fig.
4.1. The driving current can be split into two
components,
I(t) = IR + IC. The first component is the resistive
current IR which passes through the linear resistor R. It can be
calculated from Ohm's law as IR = u/R where u is the voltage across
the resistor. The second component IC charges the capacitor C. From
the definition of the capacity as C = q/u (where q is the charge and u
the voltage), we find a capacitive current
IC = C du/dt. Thus
I(t) = 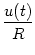 + C + C 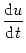 . . |
(4.2) |
We multiply (4.2) by R and introduce the time constant
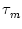 = R C of the `leaky integrator'. This yields the standard form
= R C of the `leaky integrator'. This yields the standard form
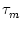 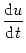 = - u(t) + R I(t) . = - u(t) + R I(t) . |
(4.3) |
We refer to u as the membrane potential and to 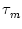 as the membrane time
constant of the neuron.
as the membrane time
constant of the neuron.
In integrate-and-fire models the form of an action potential is not described
explicitly. Spikes are formal events characterized by a `firing time' t(f).
The firing time t(f) is defined by a threshold criterion
t(f) : u(t(f)) = 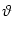 . . |
(4.4) |
Immediately after t(f), the potential is reset to a new value
ur <  ,
,
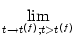 u(t) = ur . u(t) = ur . |
(4.5) |
For t > t(f) the dynamics is again given by (4.3) until the next
threshold crossing occurs. The combination of leaky integration (4.3)
and reset (4.5) defines the basic integrate-and-fire model
(Stein, 1967b). We note that, since the membrane potential is never above
threshold, the threshold condition (4.1) reduces to the criterion
(4.4), i.e., the condition on the slope
du/dt can be
dropped.
In its general version, the leaky integrate-and-fire neuron may also
incorporate an absolute refractory period, in which case we proceed as
follows. If u reaches the threshold at time t = t(f), we interrupt the
dynamics (4.3) during an absolute refractory time
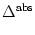 and
restart the integration at time
t(f) +
and
restart the integration at time
t(f) + 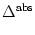 with the new initial
condition ur.
with the new initial
condition ur.
Before we continue with the definition of the integrate-and-fire model and
its variants, let us study a simple example. Suppose that the
integrate-and-fire neuron defined by (4.3)-(4.5) is stimulated
by a constant input current
I(t) = I0. For the sake of simplicity we
take the reset potential to be ur = 0.
As a first step, let us calculate the time course of the membrane potential.
We assume that a spike has occurred at t = t(1). The trajectory of
the membrane potential can be found by integrating (4.3) with the
initial condition
u(t(1)) = ur = 0. The solution is
u(t) = R I0 1 - exp 1 - exp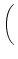 - - 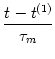 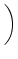 ![$\displaystyle \left.\vphantom{ 1 - \exp\left(-{t-t^{(1)} \over \tau_m} \right) }\right]$](img387.gif) . . |
(4.6) |
The membrane potential (4.6) approaches for
t
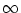 the
asymptotic value
u(
the
asymptotic value
u(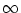 ) = R I0. For
R I0 <
) = R I0. For
R I0 <  no
further spike can occur. For
R I0 >
no
further spike can occur. For
R I0 >  , the membrane potential
reaches the threshold
, the membrane potential
reaches the threshold  at time t(2), which can be found from
the threshold condition
u(t(2)) =
at time t(2), which can be found from
the threshold condition
u(t(2)) =  or
or
Solving (4.7) for the time interval
T = t(2) - t(1) yields
T = 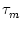 ln ln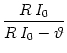 . . |
(4.8) |
After the spike at t(2) the membrane potential is again reset to ur = 0
and the integration process starts again. If the stimulus I0 remains
constant, the following spike will occur after another interval of duration
T. We conclude that for a constant input current I0, the
integrate-and-fire neuron fires regularly with period T given by
(4.8). For a neuron with absolute refractory period the firing period
T' is given by
T' = T + 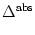 with T defined by Eq. (4.8). In
other words, the interspike interval is longer by an amount
with T defined by Eq. (4.8). In
other words, the interspike interval is longer by an amount
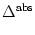 compared to that of a neuron without absolute refractory period.
compared to that of a neuron without absolute refractory period.
Figure 4.2:
A. Time course of the membrane potential of an integrate-and-fire
neuron driven by constant input current I0 = 1.5. The voltage u(t) is
normalized by the value of the threshold
 = 1. B. Gain
function. The firing rate
= 1. B. Gain
function. The firing rate 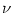 of an integrate-and-fire neuron without
(solid line) and with absolute refractoriness of
of an integrate-and-fire neuron without
(solid line) and with absolute refractoriness of
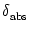 = 4 ms
(dashed line) as a function of a constant driving current I0. Current
units are normalized so that the onset of repetitive firing is at
I
= 4 ms
(dashed line) as a function of a constant driving current I0. Current
units are normalized so that the onset of repetitive firing is at
I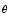 = 1. Other parameters are R = 1,
= 1. Other parameters are R = 1, 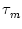 = 10ms, and ur = 0.
= 10ms, and ur = 0.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
... B}
\par\includegraphics[width=\textwidth]{pout.dat.IF-gain.eps}
\end{minipage}](img394.gif) |
The mean firing rate of a noiseless neuron is defined as 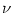 = 1/T. The
firing rate of an integrate-and-fire model with absolute refractory period
= 1/T. The
firing rate of an integrate-and-fire model with absolute refractory period
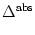 stimulated by a current I0 is therefore
stimulated by a current I0 is therefore
In Fig. 4.2B the firing rate is plotted as a function of the constant
input I0 for neurons with and without absolute refractory period.
The results of the preceding example can be generalized to arbitrary
stimulation conditions and an arbitrary reset value
ur <  . Let us
suppose that a spike has occurred at
. Let us
suppose that a spike has occurred at  . For
t >
. For
t >  the
stimulating current is I(t). The value ur will be treated as an
initial condition for the integration of (4.3), i.e.,
the
stimulating current is I(t). The value ur will be treated as an
initial condition for the integration of (4.3), i.e.,
u(t) = ur exp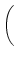 - - 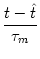 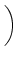 + + 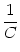  exp exp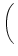 - - 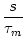 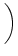 I(t - s) ds . I(t - s) ds . |
(4.10) |
This expression describes the membrane potential for t >  and is valid
up to the moment of the next threshold crossing. If
u(t) =
and is valid
up to the moment of the next threshold crossing. If
u(t) =  , the
membrane potential is reset to ur and integration restarts; see
Fig. 4.3.
, the
membrane potential is reset to ur and integration restarts; see
Fig. 4.3.
Figure 4.3:
Voltage u(t) of an integrate-and-fire model (top) driven by the input
current I(t) shown at the bottom. The input I(t) consists of a
superposition of four sinusoidal components at randomly chosen frequencies
plus a positive bias current I0 = 1.2 which drives the membrane potential
towards the threshold.
![\begin{center}
\includegraphics[height=40mm,width=80mm]{pout.dat.IF-of2.eps}
\p...
...hics[height=40mm,width=80mm]{pout.dat.IF-input.eps}
\end{center} \vspace{-5mm}](img407.gif) |
4.1.2 Nonlinear integrate-and-fire model
In a general nonlinear integrate-and-fire model, Eq. (4.3)
is replaced by
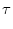 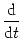 u = F(u) + G(u) I ; u = F(u) + G(u) I ; |
(4.11) |
cf. Abbott and van Vreeswijk (1993). As before, the dynamics is stopped if u reaches the
threshold  and reinitialized at u = ur. A comparison with
Eq. (4.3) shows that G(u) can be interpreted as a
voltage-dependent input resistance while
- F(u)/(u - urest) corresponds
to a voltage-dependent decay constant. A specific instance of a nonlinear
integrate-and-fire model is the quadratic
model
(Feng, 2001; Hansel and Mato, 2001; Latham et al., 2000),
and reinitialized at u = ur. A comparison with
Eq. (4.3) shows that G(u) can be interpreted as a
voltage-dependent input resistance while
- F(u)/(u - urest) corresponds
to a voltage-dependent decay constant. A specific instance of a nonlinear
integrate-and-fire model is the quadratic
model
(Feng, 2001; Hansel and Mato, 2001; Latham et al., 2000),
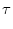 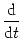 u = a0 (u - urest) (u - uc) + RI , u = a0 (u - urest) (u - uc) + RI , |
(4.12) |
with parameters a0 > 0 and
uc > urest; cf. Fig. 4.4.
For I = 0 and initial conditions u < uc, the voltage decays to the
resting potential
urest. For u > uc it increases so that an action
potential is triggered. The parameter uc can therefore be interpreted as
the critical voltage for spike initiation by a short current pulse. We will
see in the next example that the
quadratic integrate-and-fire model is closely related to the so-called
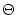 -neuron, a canonical type-I neuron model (Ermentrout, 1996; Latham et al., 2000).
-neuron, a canonical type-I neuron model (Ermentrout, 1996; Latham et al., 2000).
Figure 4.4:
Quadratic integrate-and-fire model. A. Without external current
I = 0, the membrane potential relaxes for all initial condition u < uc
to the resting potential
urest. If the membrane potential is moved
above uc, the potential increases further since
du/dt > 0. The
neuron is said to fire if u reaches the threshold
 = - 40mV.
B. A constant super-threshold current I is characterized by
the fact that
du/dt > 0 for all u. If u reaches the firing
threshold of -40mV, it is reset to -80mV. This results in repetitive
firing.
= - 40mV.
B. A constant super-threshold current I is characterized by
the fact that
du/dt > 0 for all u. If u reaches the firing
threshold of -40mV, it is reset to -80mV. This results in repetitive
firing.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...}
{\bf B}
\par\includegraphics[width=\textwidth]{quad2.thr.eps}
\end{minipage}](img408.gif) |
It is always possible to rescale the variables so that
threshold and membrane time constant are equal to unity and that the resting
potential vanishes. Furthermore, there is no need to interpret the variable
u as the membrane potential. For example, starting from the
nonlinear integrate-and-fire model Eq. (4.11), we can introduce
a new variable 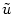 by the transformation
by the transformation
which is possible if
G(x)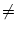 0 for all x in the integration range. In
terms of
0 for all x in the integration range. In
terms of 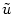 we have a new nonlinear integrate-and-fire model of the
form
we have a new nonlinear integrate-and-fire model of the
form
with
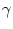 (
(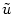 ) =
) = 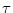 F(u)/G(u). In other words, a general
integrate-and-fire model (4.11) can always be reduced to the
standard form (4.14). By a completely analogous transformation,
we could eliminate the function F in Eq. (4.11) and move all
the dependence into a new voltage dependent G (Abbott and van Vreeswijk, 1993).
F(u)/G(u). In other words, a general
integrate-and-fire model (4.11) can always be reduced to the
standard form (4.14). By a completely analogous transformation,
we could eliminate the function F in Eq. (4.11) and move all
the dependence into a new voltage dependent G (Abbott and van Vreeswijk, 1993).
In this section, we show that there is a close relation between the quadratic integrate-and-fire
model (4.12) and the canonical type I phase model,
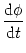 = [1 - cos = [1 - cos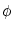 ] + ] +  I [1 + cos I [1 + cos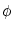 ] ; ] ; |
(4.15) |
cf. Section 3.2.4
(Strogatz, 1994; Ermentrout and Kopell, 1986; Ermentrout, 1996; Latham et al., 2000; Hoppensteadt and Izhikevich, 1997).
Let us denote by I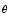 the minimal current necessary for repetitive
firing of the quadratic integrate-and-fire neuron. With a suitable shift of
the voltage scale and constant current
I = I
the minimal current necessary for repetitive
firing of the quadratic integrate-and-fire neuron. With a suitable shift of
the voltage scale and constant current
I = I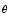 +
+  I the
equation of the quadratic neuron model can then be cast into the form
I the
equation of the quadratic neuron model can then be cast into the form
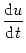 = u2 + = u2 +  I . I . |
(4.16) |
For
 I > 0 the voltage increases until it reaches the firing
threshold
I > 0 the voltage increases until it reaches the firing
threshold

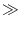 1 where it is reset to a value
ur
1 where it is reset to a value
ur 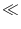 - 1. Note
that the firing times are insensitive to the actual values of firing threshold
and reset value because the solution of Eq. (4.16) grows faster than
exponentially and diverges for finite time (hyperbolic growth). The
difference in the firing times for a finite threshold of, say,
- 1. Note
that the firing times are insensitive to the actual values of firing threshold
and reset value because the solution of Eq. (4.16) grows faster than
exponentially and diverges for finite time (hyperbolic growth). The
difference in the firing times for a finite threshold of, say,
 = 10 and
= 10 and
 = 10 000 is thus negligible.
= 10 000 is thus negligible.
We want to show that the differential equation (4.16) can be
transformed into the canonical phase model (4.15) by the
transformation
To do so, we take the derivative of (4.17) and use the
differential equation (4.15) of the generic phase model. With
help of the trigonometric relations
dtan x/dx = 1/cos2(x) and
1 + cos x = cos2(x/2) we find
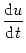 |
= |
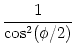 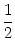 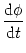 |
|
| |
= |
tan2(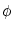 /2) + /2) +  I = u2 + I = u2 +  I . I . |
(4.18) |
Thus Eq. (4.17) with 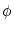 (t) given by (4.15)
is a solution to the differential equation of the quadratic integrate-and-fire
neuron. The quadratic integrate-and-fire neuron is therefore (in the limit
(t) given by (4.15)
is a solution to the differential equation of the quadratic integrate-and-fire
neuron. The quadratic integrate-and-fire neuron is therefore (in the limit

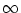 and
ur
and
ur -
- 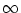 ) equivalent to the generic type I
neuron (4.15).
) equivalent to the generic type I
neuron (4.15).
4.1.3 Stimulation by Synaptic Currents
So far we have considered an isolated neuron that is stimulated by an external
current I(t). In a more realistic situation, the integrate-and-fire model
is part of a larger network and the input current I(t) is
generated by the activity of presynaptic neurons.
In the framework of the integrate-and-fire model, each presynaptic spike
generates a postsynaptic current pulse. More precisely, if the presynaptic
neuron j has fired a spike at tj(f), a postsynaptic neuron i `feels' a
current with time course
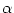 (t - tj(f)). The total input current
to neuron i is the sum over all current pulses,
(t - tj(f)). The total input current
to neuron i is the sum over all current pulses,
Ii(t) = 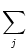 wij wij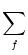 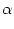 (t - tj(f)) . (t - tj(f)) . |
(4.19) |
The factor wij is a measure of the efficacy of the synapse from neuron
j to neuron i.
Though Eq. (4.19) is a reasonable model of synaptic interaction, reality
is somewhat more complicated, because the amplitude of the postsynaptic
current pulse depends on the actual value of the membrane potential ui. As
we have seen in Chapter 2, each presynaptic action potential
evokes a change in the conductance of the postsynaptic membrane with a
certain time course
g(t - t(f)). The postsynaptic current
generated by a spike at time tj(f) is thus
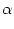 (t - tj(f)) = - g(t - tj(f)) (t - tj(f)) = - g(t - tj(f)) 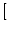 ui(t) - Esyn ui(t) - Esyn![$\displaystyle \left.\vphantom{u_i(t) - E_{\rm syn}}\right]$](img422.gif) . . |
(4.20) |
The parameter
Esyn is the reversal potential of the synapse.
The level of the reversal potential depends on the type of synapse. For
excitatory synapses,
Esyn is much larger than the resting potential.
For a voltage ui(t) close to the resting potential, we have
ui(t) < Esyn. Hence the current Ii induced by a presynaptic spike at an
excitatory synapse is positive and increases the membrane potential
4.1. The higher the voltage, the smaller the amplitude of the input
current. Note that a positive voltage
ui > urest is itself the result
of input spikes which have arrived at other excitatory synapses. Hence, there
is a saturation of the postsynaptic current and the total input current is not
just the sum of independent contributions. Nevertheless, since the reversal
potential of excitatory synapses is usually significantly above the firing
threshold, the factor
[ui - Esyn] is almost constant and saturation
can be neglected.
For inhibitory synapses, the reversal potential is close to the resting
potential. An action potential arriving at an inhibitory synapse pulls the
membrane potential towards the reversal potential
Esyn. Thus, if the
neuron is at rest, inhibitory input hardly has any effect on the membrane
potential. If the membrane potential is instead considerably above the
resting potential, then the same input has a strong inhibitory effect. This
is sometimes described as silent inhibition: inhibition is only seen if the
membrane potential is above the resting potential. Strong silent inhibition
is also called `shunting' inhibition, because a significantly reduced
resistance of the membrane potential forms a short
circuit that literally shunts excitatory input the neuron might receive from
other synapses.
The time course of the postsynaptic current 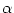 (s) introduced in
Eq. (4.19) can be defined in various ways. The simplest choice is a
Dirac
(s) introduced in
Eq. (4.19) can be defined in various ways. The simplest choice is a
Dirac  -pulse,
-pulse,
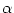 (s) = q
(s) = q  (s), where q is the total
charge that is injected in a postsynaptic neuron via a synapse with efficacy
wij = 1. More realistically, the postsynaptic current
(s), where q is the total
charge that is injected in a postsynaptic neuron via a synapse with efficacy
wij = 1. More realistically, the postsynaptic current 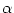 should have
a finite duration, e.g.,
as in the case of an exponential decay with time constant
should have
a finite duration, e.g.,
as in the case of an exponential decay with time constant 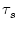 ,
,
As usual, 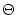 is the Heaviside step function with
is the Heaviside step function with
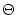 (s) = 1
for s > 0 and
(s) = 1
for s > 0 and
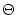 (s) = 0 else. Equation (4.21) is a simple way
to account for the low-pass characteristics of synaptic transmission;
cf. Fig. 4.1.
(s) = 0 else. Equation (4.21) is a simple way
to account for the low-pass characteristics of synaptic transmission;
cf. Fig. 4.1.
An even more sophisticated version of 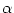 includes a finite rise time
includes a finite rise time
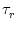 of the postsynaptic current and a transmission delay
of the postsynaptic current and a transmission delay
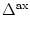 ,
,
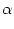 (s) = (s) = 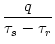  exp exp - - 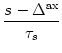  - exp - exp - - 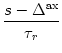  ![$\displaystyle \left.\vphantom{ \exp\left(-{s-\Delta^{\rm ax}\over \tau_s}\right) - \exp\left(-{s-\Delta^{\rm ax}\over \tau_r}\right)}\right]$](img438.gif) 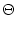 (s - (s - 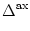 ) . ) . |
(4.22) |
In the limit of
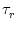
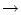
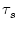 , (4.22) yields
, (4.22) yields
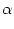 (s) = q (s) = q 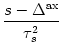 exp exp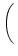 - - 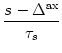 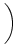  (s - (s - 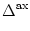 ) . ) . |
(4.23) |
In the literature, a function of the form
x exp(- x) such as (4.23)
is often called an 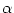 -function. While this has motivated our choice of
the symbol
-function. While this has motivated our choice of
the symbol 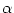 for the synaptic input current,
for the synaptic input current, 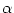 may stand for any
form of an input current pulse.
may stand for any
form of an input current pulse.





Next: 4.2 Spike response model
Up: 4. Formal Spiking Neuron
Previous: 4. Formal Spiking Neuron
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![\centerline{ \includegraphics[width=100mm]{I-Fnew.eps}}](img378.gif)
![]() and
restart the integration at time
t(f) +
and
restart the integration at time
t(f) + ![]() with the new initial
condition ur.
with the new initial
condition ur.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
... B}
\par\includegraphics[width=\textwidth]{pout.dat.IF-gain.eps}
\end{minipage}](img394.gif)
![]() = 1/T. The
firing rate of an integrate-and-fire model with absolute refractory period
= 1/T. The
firing rate of an integrate-and-fire model with absolute refractory period
![]() stimulated by a current I0 is therefore
stimulated by a current I0 is therefore
![]() . Let us
suppose that a spike has occurred at
. Let us
suppose that a spike has occurred at ![]() . For
t >
. For
t > ![]() the
stimulating current is I(t). The value ur will be treated as an
initial condition for the integration of (4.3), i.e.,
the
stimulating current is I(t). The value ur will be treated as an
initial condition for the integration of (4.3), i.e.,
![\begin{center}
\includegraphics[height=40mm,width=80mm]{pout.dat.IF-of2.eps}
\p...
...hics[height=40mm,width=80mm]{pout.dat.IF-input.eps}
\end{center} \vspace{-5mm}](img407.gif)
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...}
{\bf B}
\par\includegraphics[width=\textwidth]{quad2.thr.eps}
\end{minipage}](img408.gif)
![]() by the transformation
by the transformation
![]() the minimal current necessary for repetitive
firing of the quadratic integrate-and-fire neuron. With a suitable shift of
the voltage scale and constant current
I = I
the minimal current necessary for repetitive
firing of the quadratic integrate-and-fire neuron. With a suitable shift of
the voltage scale and constant current
I = I![]() +
+ ![]() I the
equation of the quadratic neuron model can then be cast into the form
I the
equation of the quadratic neuron model can then be cast into the form
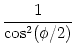
![]() (t - tj(f)). The total input current
to neuron i is the sum over all current pulses,
(t - tj(f)). The total input current
to neuron i is the sum over all current pulses,
![]() (s) introduced in
Eq. (4.19) can be defined in various ways. The simplest choice is a
Dirac
(s) introduced in
Eq. (4.19) can be defined in various ways. The simplest choice is a
Dirac ![]() -pulse,
-pulse,
![]() (s) = q
(s) = q ![]() (s), where q is the total
charge that is injected in a postsynaptic neuron via a synapse with efficacy
wij = 1. More realistically, the postsynaptic current
(s), where q is the total
charge that is injected in a postsynaptic neuron via a synapse with efficacy
wij = 1. More realistically, the postsynaptic current ![]() should have
a finite duration, e.g.,
as in the case of an exponential decay with time constant
should have
a finite duration, e.g.,
as in the case of an exponential decay with time constant ![]() ,
,
![]() includes a finite rise time
includes a finite rise time
![]() of the postsynaptic current and a transmission delay
of the postsynaptic current and a transmission delay
![]() ,
,