




Next: 4.1 Integrate-and-fire model
Up: I. Single Neuron Models
Previous: 3.4 Summary
4. Formal Spiking Neuron Models
Detailed conductance-based neuron models can reproduce electrophysiological
measurements to a high degree of accuracy, but because of their intrinsic
complexity these models are difficult to analyze. For this reason, simple
phenomenological spiking neuron models are highly popular for studies of
neural coding, memory, and network dynamics. In this chapter we discuss
formal threshold models of neuronal firing. Spikes are generated whenever the
membrane potential u crosses some threshold  from below. The
moment of threshold crossing defines the firing time t(f),
from below. The
moment of threshold crossing defines the firing time t(f),
t(f) : u(t(f)) = 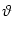 and and  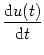 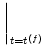 > 0 . > 0 . |
(4.1) |
Since spikes are stereotyped events they are fully characterized by their
firing time. We focus on models that are based on a single variable
u. Some well-known instances of spiking neuron models differ in the
specific way the dynamics of the variable u is defined. We start our
discussion with the integrate-and-fire neuron (Section 4.1) and turn
then to the Spike Response Model (Section 4.2). In
Section 4.3 we illustrate the relation of spiking
neuron models to conductance-based models.
Section 4.4 outlines an analytical approach for a
study of integrate-and-fire neurons with passive dendrites. As a first
application of spiking neuron models we reconsider in
Section 4.5 the problem of neuronal coding. The spiking
neuron models introduced in this chapter form the basis for the analysis of
network dynamics and learning in the following chapters.
Subsections





Next: 4.1 Integrate-and-fire model
Up: I. Single Neuron Models
Previous: 3.4 Summary
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![]() from below. The
moment of threshold crossing defines the firing time t(f),
from below. The
moment of threshold crossing defines the firing time t(f),