Next: 4.5 Application: Coding by
Up: 4. Formal Spiking Neuron
Previous: 4.3 From Detailed Models
Subsections
4.4 Multi-compartment integrate-and-fire model
The models discussed in this chapter are point neurons, i.e., models that do
not take into account the spatial structure of a real neuron. In
Chapter 2 we have already seen that the electrical properties
of dendritic trees can be described by compartmental models. In this section,
we want to show that neurons with a linear dendritic tree and a voltage
threshold for spike firing at the soma can be mapped, at least
approximatively, to the Spike Response Model.
We study an integrate-and-fire model with a passive dendritic tree described
by n compartments. Membrane resistance, core resistance,
and capacity of compartment 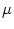 are denoted by
RT
are denoted by
RT ,
RL
,
RL , and C
, and C , respectively. The longitudinal core
resistance between compartment
, respectively. The longitudinal core
resistance between compartment 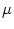 and a neighboring compartment
and a neighboring compartment 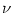 is
r
is
r
 = (RL
= (RL + RL
+ RL )/2; cf. Fig.
)/2; cf. Fig. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) . Compartment
. Compartment 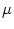 = 1 represents the soma and is equipped with
a simple mechanism for spike generation, i.e., with a threshold criterion as
in the standard integrate-and-fire model. The remaining dendritic compartments
(
2
= 1 represents the soma and is equipped with
a simple mechanism for spike generation, i.e., with a threshold criterion as
in the standard integrate-and-fire model. The remaining dendritic compartments
(
2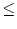
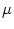
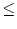 n) are passive.
n) are passive.
Each compartment
1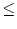
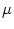
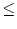 n of neuron i may receive input
Ii
n of neuron i may receive input
Ii (t) from presynaptic neurons. As a result of spike generation,
there is an additional reset current
(t) from presynaptic neurons. As a result of spike generation,
there is an additional reset current
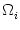 (t) at the soma. The membrane
potential Vi
(t) at the soma. The membrane
potential Vi of compartment
of compartment 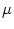 is given by
is given by
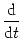 Vi Vi = = 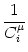  - - 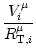 + + 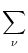 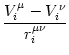 + Ii + Ii (t) - (t) - 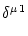 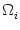 (t) (t)![$\displaystyle \left.\vphantom{ - {V_i^\mu \over R_{\text{T},i}^\mu} + \sum_\nu ...
...nu \over r_i^{\mu\nu}} + I_i^\mu (t) - \delta^{\mu\,1} \, \Omega_i (t) }\right]$](img569.gif) , , |
(4.81) |
where the sum runs over all neighbors of compartment 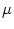 . The Kronecker
symbol
. The Kronecker
symbol
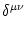 equals unity if the upper indices are equal;
otherwise, it is zero. The subscript i is the index of the neuron; the upper
indices
equals unity if the upper indices are equal;
otherwise, it is zero. The subscript i is the index of the neuron; the upper
indices 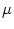 or
or 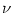 refer to compartments. Below we will identify the
somatic voltage Vi1 with the potential ui of the Spike Response Model.
refer to compartments. Below we will identify the
somatic voltage Vi1 with the potential ui of the Spike Response Model.
Equation (4.81) is a system of linear differential equations
if the external input current is independent of the membrane potential. The
solution of Eq. (4.81) can thus be formulated by means of Green's
functions
Gi
 (s) that describe the impact of an current pulse
injected in compartment
(s) that describe the impact of an current pulse
injected in compartment 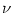 on the membrane potential of compartment
on the membrane potential of compartment 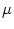 .
The solution is of the form
.
The solution is of the form
Vi (t) = (t) = 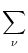 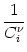 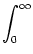 Gi Gi  (s) (s)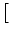 Ii Ii (t - s) - (t - s) - 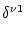 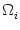 (t - s) (t - s)![$\displaystyle \left.\vphantom{ I_i^\nu (t-s) - \delta^{\nu 1} \, \Omega_i (t-s) }\right]$](img574.gif) ds . ds . |
(4.82) |
Explicit expressions for the Green's function
Gi
 (s) for arbitrary
geometry have been derived by Abbott et al. (1991) and Bressloff and Taylor (1994).
(s) for arbitrary
geometry have been derived by Abbott et al. (1991) and Bressloff and Taylor (1994).
We consider a network made up of a set of neurons described by Eq. (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) ) and a simple threshold criterion for generating spikes. We
assume that each spike tj(f) of a presynaptic neuron j evokes, for
t > tj(f), a synaptic current pulse
) and a simple threshold criterion for generating spikes. We
assume that each spike tj(f) of a presynaptic neuron j evokes, for
t > tj(f), a synaptic current pulse
 (t - tj(f)) into the postsynaptic
neuron i; cf. Eq. (4.19). The voltage dependence of the synaptic input is
thus neglected and the term
(ui - Esyn) in Eq. (4.20) is replaced
by a constant. The actual amplitude of the current pulse depends on the
strength wij of the synapse that connects neuron j to neuron i. The
total input to compartment
(t - tj(f)) into the postsynaptic
neuron i; cf. Eq. (4.19). The voltage dependence of the synaptic input is
thus neglected and the term
(ui - Esyn) in Eq. (4.20) is replaced
by a constant. The actual amplitude of the current pulse depends on the
strength wij of the synapse that connects neuron j to neuron i. The
total input to compartment  of neuron i is thus
of neuron i is thus
Ii (t) = (t) = 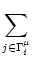 wij wij 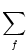 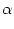 (t - tj(f)) . (t - tj(f)) . |
(4.83) |
Here,
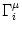 denotes the set of all neurons that have a synapse with
compartment
denotes the set of all neurons that have a synapse with
compartment 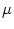 of neuron i. The firing times of neuron j are denoted by
tj(f).
of neuron i. The firing times of neuron j are denoted by
tj(f).
In the following we assume that spikes are generated at the soma in the manner
of the integrate-and-fire model. That is to say, a spike is triggered as soon
as the somatic membrane potential reaches the firing threshold,  .
After each spike the somatic membrane potential is reset to
Vi1 = ur <
.
After each spike the somatic membrane potential is reset to
Vi1 = ur <  . This is equivalent to a current pulse
. This is equivalent to a current pulse
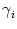 (s) = Ci1 ( (s) = Ci1 (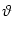 - ur) - ur) 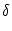 (s) , (s) , |
(4.84) |
so that the overall current due to the firing of action potentials at the soma
of neuron i amounts to
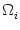 (t) = (t) = 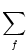 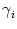 (t - ti(f)) . (t - ti(f)) . |
(4.85) |
We will refer to equations (4.82)-(4.85) together
with the threshold criterion for generating spikes as the multi-compartment
integrate-and-fire model.
Using the above specializations for the synaptic input current and the somatic
reset current the membrane potential (4.82) of compartment 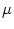 in
neuron i can be rewritten as
in
neuron i can be rewritten as
Vi (t) = (t) = 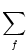 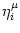 (t - ti(f)) + (t - ti(f)) + 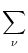 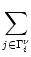 wij wij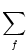 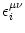 (t - tj(f)). (t - tj(f)). |
(4.86) |
with
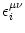 (s) (s) |
= 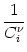 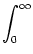 Gi Gi  (s') (s') 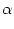 (s - s') ds' , (s - s') ds' , |
(4.87) |
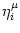 (s) (s) |
= 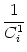 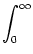 Gi Gi 1(s') 1(s') 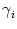 (s - s') ds'. (s - s') ds'. |
(4.88) |
The kernel
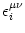 (s) describes the effect of a presynaptic
action potential arriving at compartment
(s) describes the effect of a presynaptic
action potential arriving at compartment 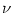 on the membrane potential of
compartment
on the membrane potential of
compartment 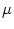 . Similarly,
. Similarly,
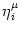 (s) describes the response of
compartment
(s) describes the response of
compartment 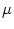 to an action potential generated at the soma.
to an action potential generated at the soma.
The triggering of action potentials depends on the somatic membrane
potential only. We define ui = Vi1,
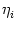 (s) =
(s) = 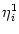 (s) and, for
j
(s) and, for
j 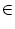
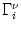 , we set
, we set
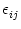 =
= 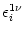 . This yields
. This yields
ui(t) = 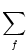 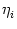 (t - ti(f)) + (t - ti(f)) + 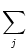 wij wij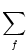 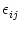 (t - tj(f)). (t - tj(f)). |
(4.89) |
As in (4.54), we use a short-term memory approximation and
truncate the sum over the 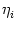 -terms. The result is
-terms. The result is
ui(t) = 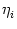 (t - (t - 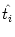 ) + ) + 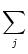 wij wij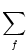 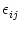 (t - tj(f)). (t - tj(f)). |
(4.90) |
where 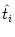 is the last firing time of neuron i. Thus, the
multi-compartment model has been reduced to the single-variable model of
Eq. (4.42). The approximation is good, if the typical inter-spike
interval is long compared to the neuronal time constants.
is the last firing time of neuron i. Thus, the
multi-compartment model has been reduced to the single-variable model of
Eq. (4.42). The approximation is good, if the typical inter-spike
interval is long compared to the neuronal time constants.
4.4.2.1 Example: Two-compartment integrate-and-fire model
Figure 4.24:
Two-compartment integrate-and-fire model. A. Response
kernel 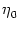 (s) of a neuron with two compartments and a fire-and-reset
threshold dynamics. The response kernel is a double exponential with time
constants
(s) of a neuron with two compartments and a fire-and-reset
threshold dynamics. The response kernel is a double exponential with time
constants
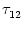 = 2ms and
= 2ms and
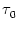 = 10 ms. The spike at s = 0 is
indicated by a vertical arrow. B. Response kernel
= 10 ms. The spike at s = 0 is
indicated by a vertical arrow. B. Response kernel
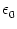 (s)
for excitatory synaptic input at the dendritic compartment with a synaptic
time constant
(s)
for excitatory synaptic input at the dendritic compartment with a synaptic
time constant
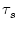 = 1 ms. The response kernel is a superposition of
three exponentials and exhibits the typical time course of an excitatory
postsynaptic potential.
= 1 ms. The response kernel is a superposition of
three exponentials and exhibits the typical time course of an excitatory
postsynaptic potential.
![\begin{minipage}{0.45\textwidth}
{\bf A}\\
\includegraphics[width=\textwidth]...
...\bf B}\\
\includegraphics[width=\textwidth]{2_comp_SRM_eps.ps}
\end{minipage}](img591.gif) |
We illustrate the Spike Response method by a simple model with two
compartments and a reset mechanism at the soma
(Rospars and Lansky, 1993). The two compartments are
characterized by a somatic capacitance C1 and a dendritic capacitance
C2 = a C1. The membrane time constant is
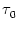 = R1 C1 = R2 C2
and the longitudinal time constant
= R1 C1 = R2 C2
and the longitudinal time constant
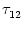 = r12 C1 C2/(C1 + C2). The neuron fires, if
V1(t) =
= r12 C1 C2/(C1 + C2). The neuron fires, if
V1(t) =  . After each firing the
somatic potential is reset to ur. This is equivalent to a current
pulse
. After each firing the
somatic potential is reset to ur. This is equivalent to a current
pulse
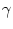 (s) = q (s) = q 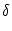 (s) , (s) , |
(4.91) |
where
q = C1 [ - ur] is the charge lost during the spike.
The dendrite receives spike trains from other neurons j and we assume that
each spike evokes a current pulse with time course
- ur] is the charge lost during the spike.
The dendrite receives spike trains from other neurons j and we assume that
each spike evokes a current pulse with time course
For the two-compartment model it is straightforward to integrate the equations
and derive the Green's function. With the Green's function we can calculate
the response kernels
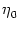 (s) =
(s) = 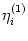 and
and
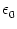 (s) =
(s) = 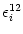 as defined in Eqs. (4.87) and (4.88); cf.
Tuckwell (1988), Bressloff and Taylor (1994). We find
as defined in Eqs. (4.87) and (4.88); cf.
Tuckwell (1988), Bressloff and Taylor (1994). We find
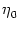 (s) (s) |
= |
- 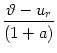 exp exp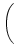 - - 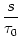   1 + a exp 1 + a exp - - 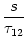  ![$\displaystyle \left.\vphantom{1 + a \, \exp\left(-{s\over \tau_{12}}
\right) }\right]$](img608.gif) , , |
(4.93) |
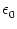 (s) (s) |
= |
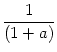 exp exp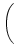 - - 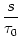 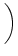  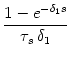 - exp - exp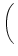 - - 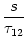 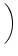 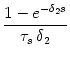 ![$\displaystyle \left.\vphantom{ {1 - e^{-{\delta_1 s}}
\over \tau_s \, \delta_1}...
...er \tau_{12}}\right)\, {1
- e^{-{\delta_2 s}} \over \tau_s\, \delta_2} }\right]$](img613.gif) , , |
|
with
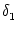 =
= 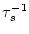 -
- 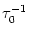 and
and
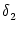 =
= 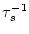 -
- 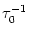 -
- 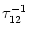 . Figure 4.24 shows the two response
kernels with parameters
. Figure 4.24 shows the two response
kernels with parameters
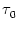 = 10 ms,
= 10 ms,
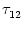 = 2 ms, and a = 10.
The synaptic time constant is
= 2 ms, and a = 10.
The synaptic time constant is
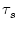 = 1 ms. The kernel
= 1 ms. The kernel
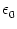 (s)
describes the voltage response of the soma to an input at the dendrite. It
shows the typical time course of an excitatory or inhibitory postsynaptic
potential. The time course of the kernel
(s)
describes the voltage response of the soma to an input at the dendrite. It
shows the typical time course of an excitatory or inhibitory postsynaptic
potential. The time course of the kernel 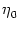 (s) is a double exponential
and reflects the dynamics of the reset in a two-compartment model.
(s) is a double exponential
and reflects the dynamics of the reset in a two-compartment model.
4.4.3 Relation to the Full Spike Response Model (*)
In the previous subsection we had to neglect the effect of spikes ti(f)
(except that of the most recent one) on the somatic membrane potential of the
neuron i itself in order to map Eq. (4.82) to the Spike Response Model. We
can do better if we allow that the response kernels 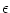 depend
explicitly on the last firing time of the presynaptic neuron. This alternative
treatment is an extension of the approach that has
already been discussed in Section 4.2.2 in the context of a
single-compartment integrate-and-fire model.
depend
explicitly on the last firing time of the presynaptic neuron. This alternative
treatment is an extension of the approach that has
already been discussed in Section 4.2.2 in the context of a
single-compartment integrate-and-fire model.
In order to account for the renewal property of the Spike Response Model we
should solve Eq. (4.81) with initial conditions
stated at the last presynaptic firing time 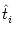 . Unfortunately, the set of
available initial conditions at
. Unfortunately, the set of
available initial conditions at 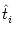 is incomplete because
only the somatic membrane potential equals ur immediately after
t =
is incomplete because
only the somatic membrane potential equals ur immediately after
t = 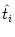 . For the membrane potential of the remaining compartments we
have to use initial conditions at t = -
. For the membrane potential of the remaining compartments we
have to use initial conditions at t = -  , but we can use a short-term
memory approximation and neglect indirect effects from earlier spikes
on the present value of the somatic membrane potential.
, but we can use a short-term
memory approximation and neglect indirect effects from earlier spikes
on the present value of the somatic membrane potential.
We start with Eq. (4.82) and split the integration over s at
s = 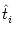 into two parts,
into two parts,
| Vi1(t) |
= 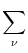 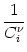 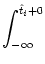 ds Gi1 ds Gi1 (t - s) (t - s)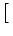 Ii Ii (s) - (s) - 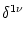 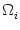 (s) (s)![$\displaystyle \left.\vphantom{ I_i^\nu(s) - \delta^{1\nu} \, \Omega_i(s) }\right]$](img623.gif) |
|
| |
+ 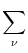 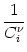 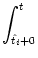 ds Gi1 ds Gi1 (t - s) Ii (t - s) Ii (s) . (s) . |
(4.94) |
The limits of the integration have been chosen to be at
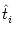 + 0 in order
to ensure that the Dirac
+ 0 in order
to ensure that the Dirac  -pulse for the reset of the membrane
potential is included in the first term.
-pulse for the reset of the membrane
potential is included in the first term.
With
Gi1 (t - s) =
(t - s) = 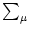 Gi1
Gi1 (t -
(t -  ) Gi
) Gi
 (
( - s), which is a general property of Green's functions, we
obtain
- s), which is a general property of Green's functions, we
obtain
| Vi1(t) |
= 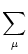 Gi1 Gi1 (t - (t -  ) )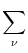 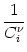 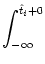 ds Gi ds Gi  ( ( - s) - s)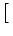 Ii Ii (s) - (s) - 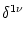 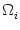 (s) (s)![$\displaystyle \left.\vphantom{ I_i^\nu(s) - \delta^{1\nu} \, \Omega_i(s) }\right]$](img623.gif) |
|
| |
+ 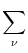 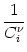 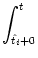 ds Gi1 ds Gi1 (t - s) Ii (t - s) Ii (s) . (s) . |
(4.95) |
With the known initial condition at the soma,
Vi1( +0) = +0) = 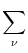 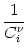 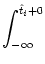 ds Gi1 ds Gi1 ( ( - s) - s) Ii Ii (s) - (s) - 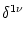 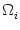 (s) (s)![$\displaystyle \left.\vphantom{ I_i^\nu(s) - \delta^{1\nu} \, \Omega_i(s) }\right]$](img623.gif) = ur , = ur , |
(4.96) |
we find
| Vi1(t) |
= Gi11(t -  ) ur ) ur |
|
| |
+ 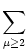 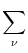 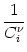 Gi1 Gi1 (t - (t -  ) )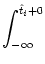 ds Gi ds Gi  ( ( - s) - s)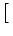 Ii Ii (s) - (s) - 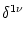 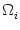 (s) (s)![$\displaystyle \left.\vphantom{ I_i^\nu(s) - \delta^{1\nu} \, \Omega_i(s) }\right]$](img623.gif) |
|
| |
+ 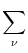 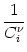 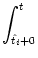 ds Gi1 ds Gi1 (t - s) Ii (t - s) Ii (s) . (s) . |
(4.97) |
The voltage reset at the soma is described by
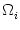 (t) = Ci1 (
(t) = Ci1 ( - ur)
- ur)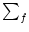
 (t - ti(f)); cf. Eqs. (4.84) and
(4.85). After shifting the terms with
(t - ti(f)); cf. Eqs. (4.84) and
(4.85). After shifting the terms with 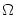 to the end and
substituting its definition, we obtain
to the end and
substituting its definition, we obtain
| Vi1(t) |
= Gi11(t -  ) ur ) ur |
|
| |
+ 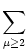 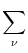 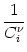 Gi1 Gi1 (t - (t -  ) )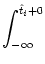 ds Gi ds Gi  ( ( - s) Ii - s) Ii (s) (s) |
|
| |
+ 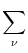 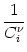 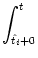 ds Gi1 ds Gi1 (t - s) Ii (t - s) Ii (s) (s) |
|
| |
+ (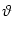 - ur) - ur)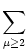 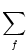 Gi1 Gi1 (t - (t -  ) Gi ) Gi 1( 1( - ti(f)) . - ti(f)) . |
(4.98) |
If we introduce
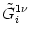 (r, s) = (r, s) = 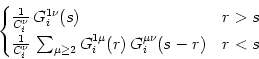 |
(4.99) |
we can collect the integrals in Eq. (4.98) and obtain
| Vi1(t) |
= Gi11(t -  ) ur ) ur |
|
| |
+ 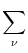 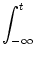 ds ds 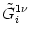 (t - (t -  , t - s) Ii , t - s) Ii (s) (s) |
|
| |
+ (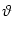 - ur) - ur)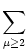 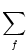 Gi1 Gi1 (t - (t -  ) Gi ) Gi 1( 1( - ti(f)) . - ti(f)) . |
(4.100) |
This expression has a clear interpretation. The first term describes the
relaxation of the somatic membrane potential in the absence of further input.
The second term accounts for external input to any of the compartments
integrated up to time t. Finally, the last term reflects an indirect
influence of previous spikes on the somatic membrane potential via other
compartments that are not reset during an action potential. In fact, the sum
over the firing times in the last term stops at the last but one action
potential since
Gi 1(
1(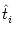 - ti(f)),
- ti(f)), 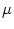 > 1, is zero if
> 1, is zero if
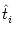 = ti(f).
= ti(f).
If we neglect the last term in Eq. (4.100), that is, if we neglect any indirect effects of previous action potentials on the somatic membrane
potential, then Eq. (4.100) can be mapped on the Spike Response Model
(4.24) by introducing kernels
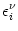 (r, s) = (r, s) = 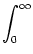 dt' dt' 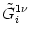 (r, t') (r, t') 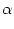 (t' - s) , (t' - s) , |
(4.101) |
and
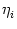 (s) = Gi11(s) ur . (s) = Gi11(s) ur . |
(4.102) |
Here, 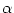 (s) describes the form of an elementary postsynaptic current;
cf. Eq. (4.83). With these definitions the somatic membrane
potential
ui(t)
(s) describes the form of an elementary postsynaptic current;
cf. Eq. (4.83). With these definitions the somatic membrane
potential
ui(t) 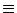 Vi1(t) of neuron i is
Vi1(t) of neuron i is
ui(t) = 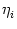 (t - (t -  ) + ) + 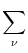 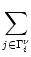 wij wij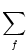 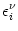 (t - (t -  , t - tj(f)) , , t - tj(f)) , |
(4.103) |
which is the equation of the Spike Response Model.





Next: 4.5 Application: Coding by
Up: 4. Formal Spiking Neuron
Previous: 4.3 From Detailed Models
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![]() are denoted by
RT
are denoted by
RT![]() ,
RL
,
RL![]() , and C
, and C![]() , respectively. The longitudinal core
resistance between compartment
, respectively. The longitudinal core
resistance between compartment ![]() and a neighboring compartment
and a neighboring compartment ![]() is
r
is
r![]()
![]() = (RL
= (RL![]() + RL
+ RL![]() )/2; cf. Fig.
)/2; cf. Fig. ![]() . Compartment
. Compartment ![]() = 1 represents the soma and is equipped with
a simple mechanism for spike generation, i.e., with a threshold criterion as
in the standard integrate-and-fire model. The remaining dendritic compartments
(
2
= 1 represents the soma and is equipped with
a simple mechanism for spike generation, i.e., with a threshold criterion as
in the standard integrate-and-fire model. The remaining dendritic compartments
(
2![]()
![]()
![]() n) are passive.
n) are passive.
![]()
![]()
![]() n of neuron i may receive input
Ii
n of neuron i may receive input
Ii![]() (t) from presynaptic neurons. As a result of spike generation,
there is an additional reset current
(t) from presynaptic neurons. As a result of spike generation,
there is an additional reset current
![]() (t) at the soma. The membrane
potential Vi
(t) at the soma. The membrane
potential Vi![]() of compartment
of compartment ![]() is given by
is given by
![]()
![]() (s) that describe the impact of an current pulse
injected in compartment
(s) that describe the impact of an current pulse
injected in compartment ![]() on the membrane potential of compartment
on the membrane potential of compartment ![]() .
The solution is of the form
.
The solution is of the form
![]() ) and a simple threshold criterion for generating spikes. We
assume that each spike tj(f) of a presynaptic neuron j evokes, for
t > tj(f), a synaptic current pulse
) and a simple threshold criterion for generating spikes. We
assume that each spike tj(f) of a presynaptic neuron j evokes, for
t > tj(f), a synaptic current pulse
![]() (t - tj(f)) into the postsynaptic
neuron i; cf. Eq. (4.19). The voltage dependence of the synaptic input is
thus neglected and the term
(ui - Esyn) in Eq. (4.20) is replaced
by a constant. The actual amplitude of the current pulse depends on the
strength wij of the synapse that connects neuron j to neuron i. The
total input to compartment
(t - tj(f)) into the postsynaptic
neuron i; cf. Eq. (4.19). The voltage dependence of the synaptic input is
thus neglected and the term
(ui - Esyn) in Eq. (4.20) is replaced
by a constant. The actual amplitude of the current pulse depends on the
strength wij of the synapse that connects neuron j to neuron i. The
total input to compartment ![]() of neuron i is thus
of neuron i is thus
![]() .
After each spike the somatic membrane potential is reset to
Vi1 = ur <
.
After each spike the somatic membrane potential is reset to
Vi1 = ur < ![]() . This is equivalent to a current pulse
. This is equivalent to a current pulse
![]() in
neuron i can be rewritten as
in
neuron i can be rewritten as
![]() (s) =
(s) = ![]() (s) and, for
j
(s) and, for
j ![]()
![]() , we set
, we set
![]() =
= ![]() . This yields
. This yields
![\begin{minipage}{0.45\textwidth}
{\bf A}\\
\includegraphics[width=\textwidth]...
...\bf B}\\
\includegraphics[width=\textwidth]{2_comp_SRM_eps.ps}
\end{minipage}](img591.gif)
![]() = R1 C1 = R2 C2
and the longitudinal time constant
= R1 C1 = R2 C2
and the longitudinal time constant
![]() = r12 C1 C2/(C1 + C2). The neuron fires, if
V1(t) =
= r12 C1 C2/(C1 + C2). The neuron fires, if
V1(t) = ![]() . After each firing the
somatic potential is reset to ur. This is equivalent to a current
pulse
. After each firing the
somatic potential is reset to ur. This is equivalent to a current
pulse
![]() depend
explicitly on the last firing time of the presynaptic neuron. This alternative
treatment is an extension of the approach that has
already been discussed in Section 4.2.2 in the context of a
single-compartment integrate-and-fire model.
depend
explicitly on the last firing time of the presynaptic neuron. This alternative
treatment is an extension of the approach that has
already been discussed in Section 4.2.2 in the context of a
single-compartment integrate-and-fire model.
![]() . Unfortunately, the set of
available initial conditions at
. Unfortunately, the set of
available initial conditions at ![]() is incomplete because
only the somatic membrane potential equals ur immediately after
t =
is incomplete because
only the somatic membrane potential equals ur immediately after
t = ![]() . For the membrane potential of the remaining compartments we
have to use initial conditions at t = -
. For the membrane potential of the remaining compartments we
have to use initial conditions at t = - ![]() , but we can use a short-term
memory approximation and neglect indirect effects from earlier spikes
on the present value of the somatic membrane potential.
, but we can use a short-term
memory approximation and neglect indirect effects from earlier spikes
on the present value of the somatic membrane potential.
![]() into two parts,
into two parts,
![]() (t - s) =
(t - s) = ![]() Gi1
Gi1![]() (t -
(t - ![]() ) Gi
) Gi![]()
![]() (
(![]() - s), which is a general property of Green's functions, we
obtain
- s), which is a general property of Green's functions, we
obtain