




Next: 4.6 Summary
Up: 4. Formal Spiking Neuron
Previous: 4.4 Multi-compartment integrate-and-fire model
Subsections
4.5 Application: Coding by Spikes
Formal spiking neuron models allow a transparent graphical discussion of
various coding principles. In this section we illustrate some
elemantary examples.
We have seen in Chapter 1.4 that the time of the first spike can
convey information about the stimulus. In order to construct a simple
example, we consider a single neuron i described by the spike response
model SRM0. The neuron receives spikes from N presynaptic neurons j
via synaptic connections that have all the same weight wij = w. There
is no external input. We assume that the last spike of neuron i occurred
long ago so that the spike after-potential 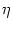 in (4.42) can be
neglected.
in (4.42) can be
neglected.
At
t = tpre, n < N presynaptic spikes are
simultaneously generated and produce a postsynaptic potential,
ui(t) = n w 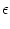 (t - tpre) . (t - tpre) . |
(4.104) |
A postsynaptic spike occurs whenever ui reaches the threshold
 . We consider the firing time ti(f) of the first output spike,
. We consider the firing time ti(f) of the first output spike,
ti(f) = min{t > tpre | ui(t) = 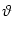 }, }, |
(4.105) |
which is a function of n. A larger numer of presynaptic spikes n results
in a postsynaptic potential with a larger amplitude so that the firing
threshold is reached earlier. The time difference
ti(f) - tpre is hence
a measure of the number of presynaptic pulses. To put it differently, the
timing of the first spike encodes the strength of the input; cf.
Fig. 4.25.
Figure 4.25:
Time-to-first-spike. The firing time tf encodes the number n1 or n2
of presynpatic spikes which have been fired synchronously at
tpre.
If there are less presynaptic spikes, the potential u rises more slowly
(dashed) and the firing occurs later. For the sake of simplicity, the
axonal delay has been set to zero;
taken from Gerstner (1998).
![\centerline{ \includegraphics[width=80mm]{SRM4.eps}}](img634.gif) |
4.5.0.2 Phase Coding
Phase coding is possible if there is a periodic background signal that can
serve as a reference. We want to show that the phase of a spike contains
information about a static stimulus h0. As before we take the model
SRM0 as a simple description of neuronal dynamics. The periodic background
signal is included into the external input. Thus we use an input potential
h(t) = h0 + h1 cos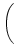 2 2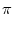 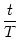  , , |
(4.106) |
where h0 is the constant stimulus and h1 is the amplitude of the
T-periodic background; cf. Eq. (4.46).
Let us consider a single neuron driven by (4.106). The membrane
potential of a SRM0 neuron is, according to (4.42) and (4.46)
u(t) = 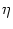 (t - (t -  ) + h(t) , ) + h(t) , |
(4.107) |
As usual  denotes the time of the most recent spike. To find the
next firing time, Eq. (4.107) has to be combined with the threshold
condition
u(t) =
denotes the time of the most recent spike. To find the
next firing time, Eq. (4.107) has to be combined with the threshold
condition
u(t) =  . We are interested in a solution where the
neuron fires regularly and with the same period as the background signal. In
this case the threshold condition reads
. We are interested in a solution where the
neuron fires regularly and with the same period as the background signal. In
this case the threshold condition reads
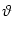 - - 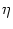 (T) = h0 + h1 cos (T) = h0 + h1 cos 2 2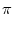 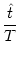  . . |
(4.108) |
For a given period T, the left-hand side has a fixed value and we can solve
for
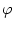 = 2
= 2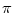
 /T. There are two solutions but only one
of them is stable. Thus the neuron has to fire at a certain phase
/T. There are two solutions but only one
of them is stable. Thus the neuron has to fire at a certain phase 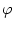 with respect to the external signal. The value of
with respect to the external signal. The value of 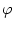 depends on the
level of the constant stimulation h0. In other words, the strength h0
of the stimulation is encoded in the phase of the spike. In
Eq. (4.108) we have moved
depends on the
level of the constant stimulation h0. In other words, the strength h0
of the stimulation is encoded in the phase of the spike. In
Eq. (4.108) we have moved 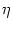 to the left-hand side in order to
suggest a dynamic threshold interpretation. A graphical interpretation of
Eq. (4.108) is given in Fig. 4.26.
to the left-hand side in order to
suggest a dynamic threshold interpretation. A graphical interpretation of
Eq. (4.108) is given in Fig. 4.26.
Figure 4.26:
Phase coding. Firing occurs whenever the total input potential
h(t) = h0 + h1 cos(2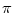 t/T) hits the dynamic threshold
t/T) hits the dynamic threshold
 -
- 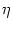 (t -
(t -  ) where
) where  is the most recent firing time;
cf. Fig. 1.11. In the presence of a periodic modulation h1
is the most recent firing time;
cf. Fig. 1.11. In the presence of a periodic modulation h1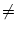 0, a
change
0, a
change
 h0 in the level of (constant) stimulation results in a
change
h0 in the level of (constant) stimulation results in a
change

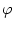 in the phase of firing;
taken from Gerstner (1998).
in the phase of firing;
taken from Gerstner (1998).
![\centerline{ \includegraphics[width=100mm]{SRM5.eps}}](img643.gif) |
4.5.0.3 Correlation coding
Let us consider two uncoupled neurons. Both receive the same constant
external stimulus
h(t) = h0. As a result, they fire regularly with
period T given by
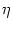 (T) = h0 as can be seen directly from
Eq. (4.108) with h1 = 0. Since the neurons are not coupled, they need not
fire simultaneously. Let us assume that the spikes of neuron 2 are shifted by
an amount
(T) = h0 as can be seen directly from
Eq. (4.108) with h1 = 0. Since the neurons are not coupled, they need not
fire simultaneously. Let us assume that the spikes of neuron 2 are shifted by
an amount  with respect to neuron 1.
with respect to neuron 1.
Suppose that, at a given moment
tpre, both neurons receive input from
a common presynaptic neuron j. This causes an additional contribution
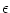 (t - tpre) to the membrane potential. If the synapse is
excitatory, the two neurons will fire slightly sooner. More importantly, the
spikes will also be closer together. In the situation sketched in Fig.
4.27 the new firing time difference
(t - tpre) to the membrane potential. If the synapse is
excitatory, the two neurons will fire slightly sooner. More importantly, the
spikes will also be closer together. In the situation sketched in Fig.
4.27 the new firing time difference
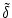 is reduced,
is reduced,
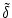 <
<  . In later chapters, we will analyze this phenomenon
in more detail. Here we just note that this effect would allow us to encode
information using the time interval between the firings of two or more
neurons.
. In later chapters, we will analyze this phenomenon
in more detail. Here we just note that this effect would allow us to encode
information using the time interval between the firings of two or more
neurons.
Figure 4.27:
The firing time difference  between two independent neurons is
decreased to
between two independent neurons is
decreased to
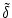 <
<  , after both neurons receive a common
excitatory input at time
tpre;
taken from Gerstner (1998).
, after both neurons receive a common
excitatory input at time
tpre;
taken from Gerstner (1998).
![\centerline{ \includegraphics[width=100mm]{SRM6.eps}}](img645.gif) |
In the previous paragraphs we have studied how a neuron can encode information
in spike timing, phase, or correlations. We now ask the inverse question,
viz., how can a neuron read out temporal information? We consider the
simplest example and study whether a neuron can distinguish synchronous from
asynchronous input. As above we make use of the simplified neuron model
SRM0 defined by (4.42) and (4.43). We will show that
synchronous input is more efficient than asynchronous input in driving a
postsynaptic neuron.
To illustrate this point, let us consider an 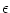 kernel of the form
kernel of the form
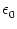 (s) = J (s) = J 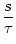 exp exp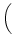 - - 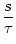   (s) . (s) . |
(4.109) |
We set J = 1 mV and 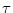 =10 ms. The function
(4.109) has a maximum value of J/e at s =
=10 ms. The function
(4.109) has a maximum value of J/e at s = 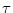 . The integral over
s is normalized to J
. The integral over
s is normalized to J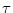 .
.
Let us consider a neuron i which receives input from 100 presynaptic neurons
j. Each presynaptic neuron fires at a rate of 10 Hz. All synapses have the
same efficacy w = 1. Let us first study the case of asynchronous input.
Different neurons fire at different times so that, on average, spikes arrive
at intervals of
 t = 1 ms. Each spike evokes a postsynaptic potential
defined by (4.109). The total membrane potential of neuron i is
t = 1 ms. Each spike evokes a postsynaptic potential
defined by (4.109). The total membrane potential of neuron i is
| ui(t) |
= |
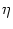 (t - (t -  ) + ) + 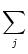 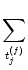 w w 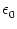 (t - tj(f)) (t - tj(f)) |
|
| |
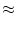 |
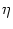 (t - (t -  ) + w ) + w 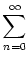 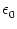 (t - n (t - n  t) t) |
(4.110) |
If neuron i has been quiescent in the recent past (
t - 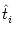
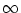 ),
then the first term on the right-hand side of (4.110) can be
neglected. The second term can be approximated by an integral over s, hence
),
then the first term on the right-hand side of (4.110) can be
neglected. The second term can be approximated by an integral over s, hence
ui(t)  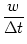 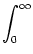 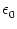 (s) ds = (s) ds = 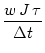 = 10 mV . = 10 mV . |
(4.111) |
If the firing threshold of the neuron is at
 = 20 mV the neuron stays
quiescent.
= 20 mV the neuron stays
quiescent.
Figure 4.28:
Potential u of a postsynaptic neuron which receives input from two groups
of presynaptic neurons. A. Spike trains of the two groups are phase
shifted with respect to each other. The total potential u does not reach
the threshold. There are no output spikes. B. Spikes from two
presynaptic groups arrive synchronously. The summed EPSPs reach the
threshold  and cause the generation of an output spike.
and cause the generation of an output spike.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\centerline{\includegraphics[width...
...{\bf B}
\par\centerline{\includegraphics[width=50mm]{fig10b.eps}} \end{minipage}](img652.gif) |
Now let us consider the same amount of input, but fired synchronously at
tj(f) = 0, 100, 200,...ms. Thus each presynaptic neuron fires as before at 10
Hz but all presynaptic neurons emit their spikes synchronously. Let us study
what happens after the first volley of spikes has arrived at t = 0. The
membrane potential of the postsynaptic neuron is
ui(t) = 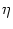 (t - (t -  ) + N w ) + N w 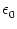 (t) (t) |
(4.112) |
where N = 100 is the number of presynaptic neurons. If the postsynaptic
neuron has not been active in the recent past, we can neglect the refractory
term 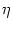 on the right-hand side of Eq. (4.112). The maximum of
(4.112) occurs at t =
on the right-hand side of Eq. (4.112). The maximum of
(4.112) occurs at t = 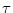 = 10 ms and has a value of
wNJ/e
= 10 ms and has a value of
wNJ/e 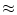 37 mV which is above threshold. Thus the postsynaptic neuron fires
before t = 10 ms. We conclude that the same number of input spikes can have
different effects depending on their level of synchrony; cf. Fig. 4.28.
37 mV which is above threshold. Thus the postsynaptic neuron fires
before t = 10 ms. We conclude that the same number of input spikes can have
different effects depending on their level of synchrony; cf. Fig. 4.28.
We will return to the question of coincidence detection, i.e., the distinction
between synchronous and asynchronous input, in the following chapter.
For a classical experimental study exploring the relevance of
temporal structure in the input, see Segundo et al. (1963).
Figure 4.29:
Sensitivity to temporal order of synaptic inputs on a dendrite. A. A
neuron is stimulated by three synaptic inputs in a sequence that starts at
the distal part of the dendrite and ends with an input close to the soma.
Since the EPSP caused by the distal input has a longer rise time than that
generated by the proximal input, the EPSPs add up coherently and the
membrane potential reaches the firing threshold  . B. If
the temporal sequence of spike inputs is reversed, the same number of input
spikes does not trigger an action potential (schematic figure).
. B. If
the temporal sequence of spike inputs is reversed, the same number of input
spikes does not trigger an action potential (schematic figure).
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...}
\par\includegraphics[width=\textwidth]{SRM-dendrite-dec-b.eps}
\end{minipage}](img653.gif) |
In neurons with a spatially extended dendritic tree the form of the
postsynaptic potential depends not only on the type, but also on the location
of the synapse; cf. Chapter 2. To be specific, let us
consider a multi-compartment integrate-and-fire model. As we have seen above
in Section 4.4, the membrane potential ui(t) can
be described by the formalism of the Spike Response Model. If the last output
spike 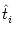 is long ago, we can neglect the refractory kernel
is long ago, we can neglect the refractory kernel
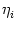 and the membrane potential is given by
and the membrane potential is given by
ui(t) = 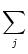 wij wij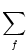 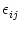 (t - tj(f)). (t - tj(f)). |
(4.113) |
cf. Eq. (4.90). The subscript ij at the 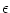 kernel takes care
of the fact that the postsynaptic potential depends on the location of the
synapse on the dendrite. Due to the low-pass characteristics of the dendrite,
synaptic input at the tip of the dendrite causes postsynaptic potentials with
a longer rise time and lower amplitude than input directly into the soma. The
total potential ui(t) depends therefore on the temporal order of the
stimulation of the synapses. An input sequence starting at the far end of the
dendrite and approaching the soma is more effective in triggering an output
spike than the same number of input spikes in reverse order; cf.
Fig. 4.29.
kernel takes care
of the fact that the postsynaptic potential depends on the location of the
synapse on the dendrite. Due to the low-pass characteristics of the dendrite,
synaptic input at the tip of the dendrite causes postsynaptic potentials with
a longer rise time and lower amplitude than input directly into the soma. The
total potential ui(t) depends therefore on the temporal order of the
stimulation of the synapses. An input sequence starting at the far end of the
dendrite and approaching the soma is more effective in triggering an output
spike than the same number of input spikes in reverse order; cf.
Fig. 4.29.





Next: 4.6 Summary
Up: 4. Formal Spiking Neuron
Previous: 4.4 Multi-compartment integrate-and-fire model
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![]() in (4.42) can be
neglected.
in (4.42) can be
neglected.
![\centerline{ \includegraphics[width=80mm]{SRM4.eps}}](img634.gif)
![\centerline{ \includegraphics[width=100mm]{SRM5.eps}}](img643.gif)
![]() (T) = h0 as can be seen directly from
Eq. (4.108) with h1 = 0. Since the neurons are not coupled, they need not
fire simultaneously. Let us assume that the spikes of neuron 2 are shifted by
an amount
(T) = h0 as can be seen directly from
Eq. (4.108) with h1 = 0. Since the neurons are not coupled, they need not
fire simultaneously. Let us assume that the spikes of neuron 2 are shifted by
an amount ![]() with respect to neuron 1.
with respect to neuron 1.
![]() (t - tpre) to the membrane potential. If the synapse is
excitatory, the two neurons will fire slightly sooner. More importantly, the
spikes will also be closer together. In the situation sketched in Fig.
4.27 the new firing time difference
(t - tpre) to the membrane potential. If the synapse is
excitatory, the two neurons will fire slightly sooner. More importantly, the
spikes will also be closer together. In the situation sketched in Fig.
4.27 the new firing time difference
![]() is reduced,
is reduced,
![]() <
< ![]() . In later chapters, we will analyze this phenomenon
in more detail. Here we just note that this effect would allow us to encode
information using the time interval between the firings of two or more
neurons.
. In later chapters, we will analyze this phenomenon
in more detail. Here we just note that this effect would allow us to encode
information using the time interval between the firings of two or more
neurons.
![\centerline{ \includegraphics[width=100mm]{SRM6.eps}}](img645.gif)
![]() kernel of the form
kernel of the form
![]() t = 1 ms. Each spike evokes a postsynaptic potential
defined by (4.109). The total membrane potential of neuron i is
t = 1 ms. Each spike evokes a postsynaptic potential
defined by (4.109). The total membrane potential of neuron i is
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\centerline{\includegraphics[width...
...{\bf B}
\par\centerline{\includegraphics[width=50mm]{fig10b.eps}} \end{minipage}](img652.gif)
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...}
\par\includegraphics[width=\textwidth]{SRM-dendrite-dec-b.eps}
\end{minipage}](img653.gif)
![]() is long ago, we can neglect the refractory kernel
is long ago, we can neglect the refractory kernel
![]() and the membrane potential is given by
and the membrane potential is given by