| (10.13) |
In this section we study synaptic plasticity at the level of individual spikes and focus on changes in the synaptic efficacy that are driven by temporal correlations between presynaptic spike arrival and postsynaptic firing.
We have seen in Chapter 1.4 that the neuronal code is still far from being fully understood. In particular, the relevance of precisely timed spikes in neuronal systems is a fundamental, yet unsolved question (Rieke et al., 1996). Nevertheless, there are neuronal systems for which the relevance of temporal information has been clearly shown. Prominent examples are the electro-sensory system of electric fish and the auditory system of barn owls (Konishi, 1993; Carr and Konishi, 1990; Konishi, 1986; Carr, 1993; Heiligenberg, 1991). If timing of spikes is important then we have to deal with the following questions: How does the timing of spikes influence weight changes? How do weight changes influence the timing of spikes?
The experiments described in the Section 10.1 show that changes of the synaptic efficacy are driven by pre- and postsynaptic activity. The amplitude and even the direction of the change depend on the relative timing of presynaptic spike arrival and postsynaptic triggering of action potentials.
In the following we develop a phenomenological model for spike-time dependent synaptic plasticity. We assume that apart from an activity-independent weight decay all changes are triggered by pre- or postsynaptic action potentials. For the sake of simplicity - and for want of detailed knowledge - we take weight changes to be instantaneous, i.e., the synaptic efficacy is a piece-wise continuous function of time with steps whenever a spike occurs. The amplitude of each step depends on the relative timing of previous spikes; cf. Fig. 10.6.
Let us first concentrate on the effect of presynaptic spikes. Each spike that arrives at the presynaptic terminal can trigger a change in the synaptic efficacy even without additional postsynaptic action potentials. In the case of so-called (non-Hebbian) presynaptic LTP, the amplitude a1pre of these changes is positive; cf. Fig. 10.6B. In addition to this non-Hebbian effect there is also a contribution to the change that depends on the time since the last postsynaptic action potential(s). In analogy to the spike response formalism of Chapter 4.2 we use an integral kernel a2pre, post to describe the amplitude of the change in the synaptic efficacy. Altogether we have
| (10.13) |
Changes in the synaptic efficacy can also be triggered by postsynaptic action potentials. Similarly to presynaptically triggered changes, the amplitude of the weight change consists of at least two contributions, viz., a non-Hebbian term a1post and the correlation term described by an integral kernel a2post, pre. Together with an activity-independent term a0 the total change in the synaptic efficacy reads
| + Sj(t) |
||
| + Si(t) |
(10.14) |
Equation (10.14) can easily be extended so as to include more
complex dependencies between pre- and postsynaptic spikes or between different
consecutive pre- or postsynaptic spikes. Analogously to Eq. (10.2) we can
include higher-order terms such as
Sj(t) ![]() a2pre, pre(s) Sj(t - s) ds and
Si(t)
a2pre, pre(s) Sj(t - s) ds and
Si(t) ![]() a2post, post(s) Si(t - s) ds that are
quadratic in pre- or postsynaptic spike trains. Nevertheless, the essence of
Hebbian synaptic plasticity is captured by the terms that are bilinear
in the pre- and postsynaptic spike train. The terms containing
a2pre, post and
a2post, pre describe the
form of the `learning window' such as the one shown in
Fig. 10.4. The kernel
a2post, pre(s), which is
usually positive, gives the amount of the weight change when a presynaptic
spike is followed by a postsynaptic action potential with delay s; cf. the
left half of the graph shown in Fig. 10.4. The kernel
a2pre, post(s) describes the right half of the graph, i.e.,
the amount of change if the timing is the other way round.
Since experimental results on spike-time dependent plasticity are usually presented
in graphical form such as in Fig. 10.4, we
define a `learning window' W as
a2post, post(s) Si(t - s) ds that are
quadratic in pre- or postsynaptic spike trains. Nevertheless, the essence of
Hebbian synaptic plasticity is captured by the terms that are bilinear
in the pre- and postsynaptic spike train. The terms containing
a2pre, post and
a2post, pre describe the
form of the `learning window' such as the one shown in
Fig. 10.4. The kernel
a2post, pre(s), which is
usually positive, gives the amount of the weight change when a presynaptic
spike is followed by a postsynaptic action potential with delay s; cf. the
left half of the graph shown in Fig. 10.4. The kernel
a2pre, post(s) describes the right half of the graph, i.e.,
the amount of change if the timing is the other way round.
Since experimental results on spike-time dependent plasticity are usually presented
in graphical form such as in Fig. 10.4, we
define a `learning window' W as
![\vbox{\hspace{0mm}
\par\hbox{{\bf A}}\hbox{ \hspace{15mm}
\includegraphics[widt...
...ox{\hspace{15mm}
\includegraphics[width=74mm]{Figs-ch-Hebbrules/Fig12c.eps}} }](img1626.gif) |
A simple choice for the learning window - and thus for the kernels a2post, pre and a2pre, post - inspired by Fig. 10.4 is
![\centerline{
\includegraphics[height=45mm]{Figs-ch-Hebbrules/pout.dat.window2.eps}
} \vspace{-15mm}](img1629.gif) |
In order to obtain a realistic description of synaptic plasticity we have to
make sure that the synaptic efficacy stays within certain bounds. Excitatory
synapses, for example, should have a positive weight and must not exceed a
maximum value of, say, wij = 1. We can implement these constraints in
Eq. (10.16) by setting
A- = wij a- and
A+ = (1 - wij) a+. The
remaining terms in Eq. (10.14) can be treated
analogously10.1. For each positive term (leading to a weight increase) we
assume a weight dependence
![]() (1 - wij), while for each negative term
(leading to weight decrease) we assume a weight dependence
(1 - wij), while for each negative term
(leading to weight decrease) we assume a weight dependence
![]() wij.
The synapse is thus no longer strengthened (or weakened) if the weight reaches
its upper (lower) bound (Kistler and van Hemmen, 2000a; van Rossum et al., 2000).
wij.
The synapse is thus no longer strengthened (or weakened) if the weight reaches
its upper (lower) bound (Kistler and van Hemmen, 2000a; van Rossum et al., 2000).
So far we have emphasized that the synaptic coupling strength is a dynamical variable that is subject to rapid changes dependent on pre- and postsynaptic activity. On the other hand, it is generally accepted that long-lasting modifications of the synaptic efficacy form the basis of learning and memory. How can fast dynamical properties be reconciled with long-lasting modifications?
Most learning theories dealing with artificial neural networks concentrate on the induction of weight changes. As soon as the `learning session' is over, synaptic plasticity is `switched off' and weights are taken as fixed parameters. In biological systems, a similar mechanism can be observed during development. There are critical periods in the early life time of an animal where certain synapses show a form of plasticity that is `switched off' after maturation (Crepel, 1982). The majority of synapses, especially those involved in higher brain functions, however, keep their plasticity throughout their life. At first glance there is thus the risk that previously stored information is simply overwritten by new input (`palimpsest property'). Grossberg has coined the term `stability-plasticity dilemma' for this problem (Carpenter and Grossberg, 1987; Grossberg, 1987).
To address these questions, Fusi et al. (2000) have studied the problem of the consolidation of synaptic weights. They argue that bistability of synaptic weights can solve the stability-plasticity dilemma. More specifically, the dynamics of synaptic efficacies is characterized by two stable fixed points at wij = 0 and wij = 1. In the absence of stimulation the synaptic weight will thus settle down at either one of these values. Pre- or postsynaptic activity can lead to a transition from one fixed point to the other, but only if the duration of the stimulus presentation or its amplitude exceeds a certain threshold. In other words, synapses can be switched on or off but this will happen only for those synapses where the learning threshold is exceeded. Learning thus affects only a few synapses so that previously stored information is mostly preserved.
In the framework of Eq. (10.14), such a dynamics for synaptic weights can be implemented by setting
In Eq. (10.14) weight changes occur instantaneously at the moment of presynaptic spike arrival or postsynaptic firing. In this subsection we will develop a slightly more general equation for the evolution of synaptic weights. The approach taken in this section can be seen as a generalization of the Taylor expansion in the rate model of Section 10.2 to the case of spiking neurons.
We recall that we started our formulation of rate-based Hebbian learning from a general formula
The internal state of spiking neurons (e.g., integrate-and-fire or Spike Response Model neurons) is characterized by the membrane potential u which in turn depends on the input and the last output spike. The generalization of Eq. (10.18) to the case of spiking neurons is therefore
In analogy to the approach taken in Section 10.2, we now expand
the right-hand side of Eq. (10.19) about the resting state
uipost = ujpre = urest in a Volterra series
(Palm and Poggio, 1977; van Hemmen et al., 2000; Volterra, 1959). For the sake of
simplicity we shift the voltage scale so that
urest = 0. We find
| = | a0(wij) + |
||
| + |
(10.20) | ||
| + |
In order to establish a connection with various other formulations of
spike-based learning rules, we consider the time course of the pre- and
postsynaptic membrane potential in more detail. At the presynaptic terminal,
the membrane potential is most of the time at rest, except when an action
potential arrives. Since the duration of each action potential is short, the
presynaptic membrane potential can be approximated by a train of ![]() functions
functions
The situation at the postsynaptic site is somewhat more complicated. For the simple spike response model SRM0, the membrane potential can be written as
For a further simplification of Eq. (10.20), we need to make
some approximations. Specifically we will explore two different approximation
schemes. In the first scheme, we suppose that the dominating term on the
right-hand side of Eq. (10.22) is the back propagating action
potential, while in the second scheme we neglect ![]() and consider h as
the dominant term. Let us discuss both approximations in turn.
and consider h as
the dominant term. Let us discuss both approximations in turn.
We assume that the back propagating action potential is sharply peaked, i.e.,
it has a large amplitude and short duration. In this case, the membrane
potential of the postsynaptic neuron is dominated by the back propagating
action potential and the term h(t) in Eq. (10.22) can be neglected.
Furthermore ![]() can be approximated by a
can be approximated by a ![]() function. The membrane
potential at the postsynaptic site reduces then to a train of pulses,
function. The membrane
potential at the postsynaptic site reduces then to a train of pulses,
If we insert Eqs. (10.21) and (10.23) into Eq. (10.20) we find
In typical plasticity experiments, the synaptic weight is monitored every few
hundred milliseconds so that the exact time course of the functions,
![]() ,
,
![]() and
and
![]() is not measured. To establish
the connection to Eq. (10.14), we now assume that the weight
changes are rapid compared to the time scale of weight monitoring. In other
words, we make the replacement
is not measured. To establish
the connection to Eq. (10.14), we now assume that the weight
changes are rapid compared to the time scale of weight monitoring. In other
words, we make the replacement
| apre1 |
(10.24) | ||
| apost1 |
(10.25) |
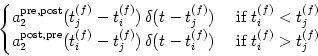 |
(10.26) |
In the second approximation scheme, we assume that the membrane potential at the location of the synapse is dominated by the slowly varying potential hi(t). This is, for example, a valid assumption in voltage-clamp experiments where the postsynaptic neuron is artificially kept at a constant membrane potential hpost. This is also a good approximation for synapses that are located far away from the soma on a passive dendrite, so that the back propagation of somatic action potentials is negligible.
Let us consider a voltage clamp experiment where hi(t) is kept at a
constant level
hpost. As before, we suppose that weight changes are
rapid. If we insert
uprej(t) = ![]()
![]() (t - tj(f)) and
uipost(t) = hpost into Eq. (10.20), we find
(t - tj(f)) and
uipost(t) = hpost into Eq. (10.20), we find
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.