In this section we perform a systematic reduction of the four-dimensional Hodgkin-Huxley model to two dimensions. To do so, we have to eliminate two of the four variables. The essential ideas of the reduction can also be applied to detailed neuron models that may contain many different ion channels. In this case, more than two variables would have to be eliminated, but the procedure would be completely analogous (Kepler et al., 1992).
We focus on the Hodgkin-Huxley model
discussed in
Chapter 2.2 and start with two qualitative observations. First, we
see from Fig. 2.3B that the time scale of the dynamics of the
gating variable m is much faster than that of the variables n, h, and
u. This suggests that we may treat m as an instantaneous variable.
The variable m in
the ion current equation (2.5)
of the Hodgkin-Huxley model can therefore be
replaced by its steady-state value,
m(t)![]() m0[u(t)]. This is what we call a quasi steady state
approximation.
m0[u(t)]. This is what we call a quasi steady state
approximation.
Second, we see from Fig. 2.3B that the time constants ![]() (u)
and
(u)
and ![]() (u) are roughly the same, whatever the voltage u. Moreover, the
graphs of n0(u) and 1 - h0(u) in Fig. 2.3A are rather similar.
This suggests that we may approximate the two variables n and (1 - h) by a
single effective variable w. To keep the formalism slightly more general we
use a linear approximation
(b - h)
(u) are roughly the same, whatever the voltage u. Moreover, the
graphs of n0(u) and 1 - h0(u) in Fig. 2.3A are rather similar.
This suggests that we may approximate the two variables n and (1 - h) by a
single effective variable w. To keep the formalism slightly more general we
use a linear approximation
(b - h) ![]() a n with some constants a, b and
set
w = b - h = a n. With h = b - w, n = w/a, and m = m0(u), equations
(2.4) - (2.5) become
a n with some constants a, b and
set
w = b - h = a n. With h = b - w, n = w/a, and m = m0(u), equations
(2.4) - (2.5) become
Morris and Lecar (1981) proposed a two-dimensional description of neuronal spike
dynamics. A first equation describes the evolution of the membrane potential
u, the second equation the evolution of a slow `recovery' variable
![]() . In dimensionless variables, the Morris-Lecar equations read
. In dimensionless variables, the Morris-Lecar equations read
The equilibrium functions shown in Fig. 2.3A typically have a
sigmoidal shape. It is reasonable to approximate the voltage dependence by
The Morris-Lecar model (3.4)-(3.8) gives a phenomenological description of action potentials. Action potentials occur, if the current I is sufficiently strong. We will see later on that the firing threshold in the Morris-Lecar model can be discussed by phase plane analysis.
FitzHugh and Nagumo where probably the first to propose that, for a discussion
of action potential generation, the four equations of Hodgkin and Huxley can
be replaced by two, i.e., Eqs. (3.2)
and (3.3). They obtained
sharp pulse-like oscillations reminiscent of trains of action potentials by
defining the functions F(u, w) and G(u, w) as
The reduction of the Hodgkin-Huxley model to Eqs. (3.2) and (3.3) presented in this paragraph is inspired by the geometrical treatment of Rinzel (1985); see also the slightly more general method of Abbott and Kepler (1990) and Kepler et al. (1992).
The overall aim of the approach is to replace the variables n and h in the Hodgkin-Huxley model by a single effective variable w. At each moment of time, the values (n(t), h(t)) can be visualized as points in the two-dimensional plane spanned by n and h; cf. Fig. 3.1. We have argued above that the time course of the variable n is expected to be similar to that of 1 - h. If, at each time, n was equal to 1 - h, then all possible points (n, h) would lie on the straight line h = 1 - n passing through the points (0, 1) and (1, 0) of the plane. To keep the model slightly more general we allow for an arbitrary line h = b - a n which passes through (0, b) and (1, b - a). It would be unreasonable to expect that all points (n(t), h(t)) that occur during the temporal evolution of the Hodgkin-Huxley model fall exactly on that line. The reduction of the number of variables is achieved by a projection of those points onto the line. The position along the line h = b - a n gives the new variable w; cf. Fig. 3.1. The projection is the essential approximation during the reduction.
![\includegraphics[width=55mm]{reduction.eps}](img279.gif) |
To perform the projection, we will proceed in three steps. A minimal
condition for the projection is that the approximation introduces no error
while the neuron is at rest. As a first step, we therefore shift the origin
of the coordinate system to the rest state and introduce new variables
Second, we turn the coordinate system by an angle ![]() which is determined
as follows. For a given constant voltage u, the dynamics of the gating
variables n and h approaches the equilibrium values
(n0(u), h0(u)).
The points
(n0(u), h0(u)) as a function of u define a curve in the
two-dimensional plane. The slope of the curve at
u = urest yields the
turning angle
which is determined
as follows. For a given constant voltage u, the dynamics of the gating
variables n and h approaches the equilibrium values
(n0(u), h0(u)).
The points
(n0(u), h0(u)) as a function of u define a curve in the
two-dimensional plane. The slope of the curve at
u = urest yields the
turning angle ![]() via
via
tan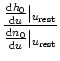 . . |
(3.12) |
Third, we set z2 = 0 and retain only the coordinate z1 along ![]() .
The inverse transform,
.
The inverse transform,
In principle, z1 can directly be used as the new effective variable. From (3.13) we find the differential equation
| (3.17) |
To see the relation to Eqs. (3.1) and (3.3), it is convenient to rescale z1 and define
| w0(u) = - sin |
(3.21) |
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.