




Next: 5.5 Diffusive noise
Up: 5. Noise in Spiking
Previous: 5.3 Escape noise
5.4 Slow noise in the parameters
In one of the previous examples (`Motivating sigmoidal escape rates' in
Section 5.3.1), a new value of the threshold was chosen
at each time step; cf. Eq. (5.49). If time steps are
short enough, such an approach is closely related to escape rate models. A
completely different class of noise models can be constructed if the value of
a parameter is changed after each spike. Thus between two spikes the
noise is `frozen' so that the value of the fluctuating parameter does not
change. In other words, the noise is slow compared to the fast neuronal
dynamics. In principle, any of the neuronal parameters such as threshold,
membrane time constant, or length of the refractory period, can be subject
to this type of noise (Gerstner, 2000b; Lansky and Smith, 1989; Gestri, 1978; Knight, 1972a).
In this section
we want to show how to analyze such slow variations and calculate the interval
distribution. We emphasize that these `slow' noise models cannot be mapped
onto an escape rate formalism.
Figure 5.11:
Slow noise in the parameters. After each spike either the reset value (A) or the firing threshold (B) is set to a new randomly chosen
value.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\hfill\includegraphics[height=35mm...
...r\hfill\includegraphics[height=35mm,width=60mm]{slownoise-b.eps}
\end{minipage}](img799.gif) |
To keep the arguments simple, we will concentrate on noise in the formulation
of reset and refractoriness. We assume an exponential refractory kernel,
with time constant 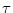 . In order to introduce noise, we suppose that the
amount
. In order to introduce noise, we suppose that the
amount 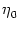 of the reset depends on a stochastic variable r,
of the reset depends on a stochastic variable r,
where
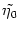 < 0 is a fixed parameter and r is a random variable
with zero mean. In the language of the integrate-and-fire neuron, we can
describe the effect of r as a stochastic component in the value of the reset
potential.
< 0 is a fixed parameter and r is a random variable
with zero mean. In the language of the integrate-and-fire neuron, we can
describe the effect of r as a stochastic component in the value of the reset
potential.
In the `noisy reset' model, firing is given by
the threshold condition
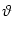 = u(t| = u(t| , r) = , r) = 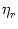 (t - (t -  ) + ) + 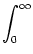 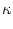 (t - (t -  , s) I(t - s) ds , , s) I(t - s) ds , |
(5.66) |
where
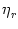 (t -
(t -  ) =
) = 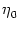 (r) exp[- (t -
(r) exp[- (t -  )/
)/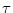 ]. Since u
depends on the current value of r, we have written
u(t|
]. Since u
depends on the current value of r, we have written
u(t| , r) instead of
u(t|
, r) instead of
u(t| ). Let us write
T(
). Let us write
T( , r) for the next interval of a neuron
which has fired at
, r) for the next interval of a neuron
which has fired at  and was reset with a stochastic value r, i.e.,
and was reset with a stochastic value r, i.e.,
T( , r) = min , r) = min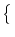 t - t -  | u(t| | u(t| , r) = , r) = 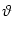 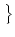 . . |
(5.67) |
If r is drawn from a Gaussian distribution
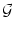
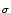 (r) with
variance
(r) with
variance
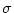
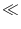
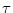 , the interval distribution is
, the interval distribution is
PI(t |  ) = ) = 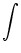 dr dr 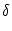 [t - [t -  - T( - T( , r)] , r)] 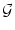 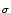 (r) . (r) . |
(5.68) |
Let us now evaluate the interval distribution (5.68) for the variant
SRM0 of the Spike Response Model,
u(t| , r) = , r) = 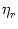 (t - (t -  ) + h(t) , ) + h(t) , |
(5.69) |
with constant input potential
h(t) = h0. First we show that a stochastic
reset according to (5.65) with r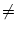 0 shifts
the refractory kernel horizontally along the time axis. To see this, let us
consider a neuron that has fired its last spike at
0 shifts
the refractory kernel horizontally along the time axis. To see this, let us
consider a neuron that has fired its last spike at  and has been
reset with a certain value r. The refractory term is
and has been
reset with a certain value r. The refractory term is
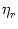 (t - (t -  ) = ) = 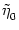 exp[- (t - exp[- (t -  - r)/ - r)/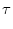 ] , ] , |
(5.70) |
which is identical to that of a noiseless neuron that
has fired its last spike at
t' =  + r. Given the constant input
potential h0, a noise-free SRM0 neuron would fire regularly with period
T0. A noisy neuron that was reset with value r is delayed by a time r
and fires therefore after an interval
T(
+ r. Given the constant input
potential h0, a noise-free SRM0 neuron would fire regularly with period
T0. A noisy neuron that was reset with value r is delayed by a time r
and fires therefore after an interval
T( , r) = T0 + r. Integration
of Eq. (5.68) yields the interval distribution
, r) = T0 + r. Integration
of Eq. (5.68) yields the interval distribution
P0(t -  ) = ) = 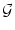 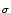 (t - (t -  - T0) . - T0) . |
(5.71) |
Thus, the Gaussian distribution
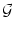
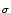 (r) of the noise variable r maps
directly to a Gaussian distribution of the intervals around the mean T0.
For a detailed discussion of the relation between the distribution
of reset values
and the interval distribution
P0(t -
(r) of the noise variable r maps
directly to a Gaussian distribution of the intervals around the mean T0.
For a detailed discussion of the relation between the distribution
of reset values
and the interval distribution
P0(t -  )
of leaky integrate-and-fire neurons,
see Lansky and Smith (1989).
)
of leaky integrate-and-fire neurons,
see Lansky and Smith (1989).
Even though stochastic reset is not a realistic noise model for individual
neurons, noise in the parameter values can approximate inhomogeneous
populations of neurons where parameters vary
from one neuron to the next (Wilson and Cowan, 1972; Knight, 1972a). Similarly, a
fluctuating background input that changes slowly compared to the typical
interspike interval can be considered as a slow change in the value of the
firing threshold. More generally, noise with a cut-off frequency smaller than
the typical firing rate can be described as slow noise in the parameters.





Next: 5.5 Diffusive noise
Up: 5. Noise in Spiking
Previous: 5.3 Escape noise
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\hfill\includegraphics[height=35mm...
...r\hfill\includegraphics[height=35mm,width=60mm]{slownoise-b.eps}
\end{minipage}](img799.gif)
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\hfill\includegraphics[height=35mm...
...r\hfill\includegraphics[height=35mm,width=60mm]{slownoise-b.eps}
\end{minipage}](img799.gif)