




Next: 5.6 The subthreshold regime
Up: 5. Noise in Spiking
Previous: 5.4 Slow noise in
Subsections
5.5 Diffusive noise
The integrate-and-fire model is, in its simplest form, defined by a
differential equation
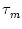 du/dt = - u + R I(t) where
du/dt = - u + R I(t) where 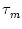 is the membrane time constant, R the input resistance, and I the input
current. The standard procedure of implementing noise in such a differential
equation is to add a `noise term',
is the membrane time constant, R the input resistance, and I the input
current. The standard procedure of implementing noise in such a differential
equation is to add a `noise term', 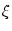 (t), on the right-hand side. The noise
term
(t), on the right-hand side. The noise
term 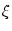 is a stochastic process called `Gaussian white noise' characterized
by its expectation value,
is a stochastic process called `Gaussian white noise' characterized
by its expectation value,
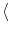
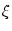 (t)
(t)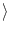 = 0, and the autocorrelation
= 0, and the autocorrelation
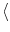 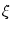 (t) (t) 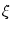 (t') (t')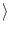 = = 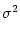 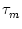 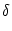 (t - t') , (t - t') , |
(5.72) |
where 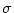 is the amplitude of the noise
and
is the amplitude of the noise
and 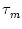 the membrane time constant of the neuron.
The result is a stochastic
differential equation,
the membrane time constant of the neuron.
The result is a stochastic
differential equation,
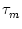 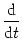 u(t) = - u(t) + R I(t) + u(t) = - u(t) + R I(t) + 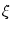 (t) , (t) , |
(5.73) |
i.e., an equation for a stochastic
process (Ornstein-Uhlenbeck process); cf. van Kampen (1992).
The neuron is said to fire an action potential whenever the membrane
potential u reaches the threshold 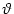 ; cf.
Fig. 5.12. We will refer to Eq. (5.73) as the Langevin
equation of the noisy integrate-and-fire model. The analysis of
Eq. (5.73) in the presence of the threshold
; cf.
Fig. 5.12. We will refer to Eq. (5.73) as the Langevin
equation of the noisy integrate-and-fire model. The analysis of
Eq. (5.73) in the presence of the threshold 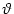 is the topic of
this section. Before we start with the discussion of Eq. (5.73), we
indicate how the noise term
is the topic of
this section. Before we start with the discussion of Eq. (5.73), we
indicate how the noise term 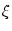 (t) can be motivated by stochastic spike
arrival.
(t) can be motivated by stochastic spike
arrival.
Figure 5.12:
Noisy integration. A stochastic contribution in the input current
of an integrate-and-fire neuron causes the membrane potential to drift away
from the reference trajectory (thick solid line). The neuron fires if the
noisy trajectory (thin line) hits the threshold 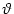 (schematic figure).
(schematic figure).
![\centerline{\includegraphics[width=60mm]{noise-diff-mod.eps}}](img812.gif) |
A typical neuron, e.g., a pyramidal cell in the vertebrate cortex, receives
input spikes from thousands of other neurons, which in turn receive input from
their presynaptic neurons and so forth; see Fig. 5.13.
It is obviously impossible to incorporate all neurons in the brain into one
huge network model. Instead, it is reasonable to focus on a specific subset
of neurons, e.g., a column in the visual cortex, and describe input from other
parts of the brain as a stochastic background activity.
Figure 5.13:
Each neuron receives input spikes from a large number of presynaptic
neurons. Only a small portion of the input comes from neurons within
the model network; other input is described as stochastic spike arrival.
![\centerline{\includegraphics[width=100mm]{spike-input2a.eps}}](img813.gif) |
Let us consider an integrate-and-fire neuron that is part of a large network.
Its input consists of (i) an external input
Iext(t); (ii) input
spikes tj(f) from other neurons j of the network; and (iii) stochastic
spike arrival tk(f) due to the background activity in other parts of the
brain. The membrane potential u evolves according to
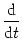 u = - u = - 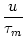 + + 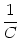 Iext(t) + Iext(t) + 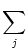 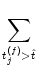 wj wj 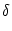 (t - tj(f)) + (t - tj(f)) + 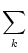 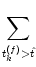 wk wk 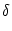 (t - tk(f)) , (t - tk(f)) , |
(5.74) |
where 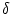 is the Dirac
is the Dirac 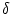 function and wj is the coupling to
other presynaptic neurons j in the network. Input from background neurons
is weighted by the factor wk. Firing times tk(f) of a background neuron
k are generated by a Poisson process with mean rate
function and wj is the coupling to
other presynaptic neurons j in the network. Input from background neurons
is weighted by the factor wk. Firing times tk(f) of a background neuron
k are generated by a Poisson process with mean rate 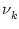 .
Eq. (5.74) is called Stein's model
(Stein, 1967b,1965).
.
Eq. (5.74) is called Stein's model
(Stein, 1967b,1965).
In Stein's model, each input spike generates a postsynaptic potential
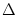 u(t) = wj
u(t) = wj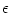 (t - tj(f)) with
(t - tj(f)) with
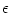 (s) = e-s/
(s) = e-s/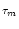
 (s),
i.e., the potential jumps upon spike arrival by an amount wj and decays
exponentially thereafter. It is straightforward to generalize the model so as
to include a synaptic time constant and work with arbitrary postsynaptic
potentials
(s),
i.e., the potential jumps upon spike arrival by an amount wj and decays
exponentially thereafter. It is straightforward to generalize the model so as
to include a synaptic time constant and work with arbitrary postsynaptic
potentials
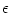 (s) that are generated by stochastic spike arrival; cf. Fig. 5.14A.
(s) that are generated by stochastic spike arrival; cf. Fig. 5.14A.
We consider stochastic spike arrival at rate 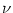 . Each input spike evokes a
postsynaptic potential
w0
. Each input spike evokes a
postsynaptic potential
w0 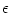 (s). The input statistics is assumed
to be Poisson, i.e., firing times are independent. Thus, the input spike
train,
(s). The input statistics is assumed
to be Poisson, i.e., firing times are independent. Thus, the input spike
train,
S(t) = 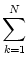 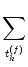 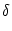 (t - tk(f)) , (t - tk(f)) , |
(5.75) |
that arrives at neuron i is a random process with expectation
and autocorrelation
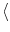 S(t) S(t') S(t) S(t')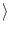 - - 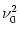 = N = N 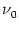 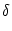 (t - t') ; (t - t') ; |
(5.77) |
cf. Eq. (5.36).
Figure 5.14:
Input spikes arrive stochastically (lower panel) at a mean rate of 1 kHz.
A. Each input spike evokes an EPSP
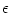 (s)
(s) 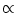 s exp(- s/
s exp(- s/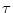 ) with
) with 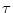 = 4 ms. The first EPSP (the one generated by the
spike at t = 0) is plotted. The EPSPs of all spikes sum up and result in a
fluctuating membrane potential u(t). B. Continuation of the
simulation shown in A. The horizontal lines indicate the mean (dotted
line) and the standard deviation (dashed lines) of the membrane potential.
= 4 ms. The first EPSP (the one generated by the
spike at t = 0) is plotted. The EPSPs of all spikes sum up and result in a
fluctuating membrane potential u(t). B. Continuation of the
simulation shown in A. The horizontal lines indicate the mean (dotted
line) and the standard deviation (dashed lines) of the membrane potential.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[height=35mm,width...
...udegraphics[width=60mm]{pout.dat.spikes-all.eps}
\end{minipage} \vspace{-35mm}](img823.gif) |
We suppose that the input is weak so that the neuron does not reach its firing
threshold. Hence, we can savely neglect both threshold and reset. Using the
definition of the random process S we find for the
membrane potential
u(t) = w0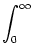 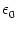 (s) S(t - s) ds . (s) S(t - s) ds . |
(5.78) |
We are interested in the mean potential
u0 = 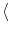 u(t)
u(t)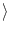 and the
variance
and the
variance
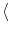
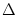 u2
u2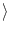 =
= 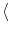 [u(t) - u0]2
[u(t) - u0]2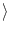 . Using
Eqs. (5.76) and (5.77) we find
. Using
Eqs. (5.76) and (5.77) we find
and
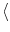 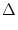 u2 u2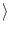 |
= w02 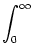 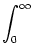 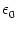 (s) (s) 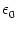 (s') (s') 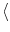 S(t) S(t') S(t) S(t')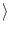 ds ds' - u02 ds ds' - u02 |
|
| |
= w02 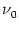 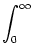 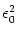 (s) ds . (s) ds . |
(5.80) |
In Fig. 5.14 we have simulated a neuron which receives input
from N = 100 background neurons with rate
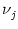 = 10 Hz. The total spike
arrival rate is therefore
= 10 Hz. The total spike
arrival rate is therefore 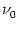 = 1 kHz. Each spike evokes an EPSP
w0
= 1 kHz. Each spike evokes an EPSP
w0 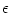 (s) = 0.1 (s/
(s) = 0.1 (s/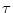 ) exp(- s/
) exp(- s/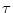 ) with
) with 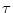 = 4ms. The
evaluation of Eqs. (5.79) and (5.80) yields u0 = 0.4 and
= 4ms. The
evaluation of Eqs. (5.79) and (5.80) yields u0 = 0.4 and
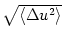 = 0.1.
= 0.1.
Mean and fluctuations for Stein's model can be derived by evaluation of
Eqs. (5.79) and (5.80) with
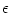 (s) = e-s/
(s) = e-s/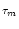 . The result is
. The result is
| u0 |
= |
w0 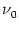 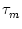 |
(5.81) |
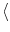 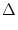 u2 u2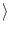 |
= |
0.5 w02 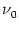 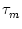 |
(5.82) |
Note that with excitation alone, as considered here, mean and variance cannot
be changed independently. As we will see in the next example, a combination
of excitation and inhibition allows us to increase the variance while keeping
the mean of the potential fixed.
5.5.1.2 Example: Balanced excitation and inhibition
Let us suppose that an integrate-and-fire neuron defined by
Eq. (5.74) with 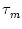 = 10ms receives input from 100 excitatory
neurons (
wk = + 0.1) and 100 inhibitory neurons (
wk = - 0.1). Each
background neuron k fires at a rate of
= 10ms receives input from 100 excitatory
neurons (
wk = + 0.1) and 100 inhibitory neurons (
wk = - 0.1). Each
background neuron k fires at a rate of 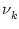 = 10Hz. Thus, in each
millisecond, the neuron receives on average one excitatory and one inhibitory
input spike. Each spike leads to a jump of the membrane potential of ±0.1. The trajectory of the membrane potential is therefore similar to that
of a random walk; cf. Fig. 5.15A. If, in
addition, a constant stimulus
Iext = I0 > 0 is applied so that the
mean membrane potential (in the absence of the background spikes) is just
below threshold, then the presence of random background spikes may drive u
towards the firing threshold. Whenever
u
= 10Hz. Thus, in each
millisecond, the neuron receives on average one excitatory and one inhibitory
input spike. Each spike leads to a jump of the membrane potential of ±0.1. The trajectory of the membrane potential is therefore similar to that
of a random walk; cf. Fig. 5.15A. If, in
addition, a constant stimulus
Iext = I0 > 0 is applied so that the
mean membrane potential (in the absence of the background spikes) is just
below threshold, then the presence of random background spikes may drive u
towards the firing threshold. Whenever
u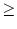
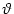 , the membrane
potential is reset to ur = 0.
, the membrane
potential is reset to ur = 0.
Figure 5.15:
A. Voltage trajectory of an integrate-and-fire neuron (
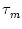 = 10 ms, ur = 0) driven by
stochastic excitatory and inhibitory spike input at
= 10 ms, ur = 0) driven by
stochastic excitatory and inhibitory spike input at
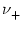 =
= 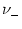 = 1
kHz. Each input spike causes a jump of the membrane potential by
w± = ±0.1. The neuron is biased by a constant current I0 = 0.8 which
drives the membrane potential to a value just below the threshold of
= 1
kHz. Each input spike causes a jump of the membrane potential by
w± = ±0.1. The neuron is biased by a constant current I0 = 0.8 which
drives the membrane potential to a value just below the threshold of
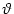 = 1 (horizontal line). Spikes are marked by vertical lines. B. Similar plot as in A except that the jumps are smaller (
w± = ±0.025) while rates are higher (
= 1 (horizontal line). Spikes are marked by vertical lines. B. Similar plot as in A except that the jumps are smaller (
w± = ±0.025) while rates are higher (
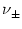 = 16 kHz).
= 16 kHz).
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[height=35mm,width...
...ludegraphics[height=35mm,width=60mm]{pout.dat.IF-of-t-diff2.eps}
\end{minipage}](img828.gif) |
We note that the mean of the stochastic background input vanishes since
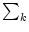 wk
wk 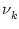 = 0. Using the same arguments as in the previous
example, we can convince ourselves that the stochastic arrival of background
spikes generates fluctuations of the voltage with variance
= 0. Using the same arguments as in the previous
example, we can convince ourselves that the stochastic arrival of background
spikes generates fluctuations of the voltage with variance
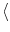 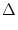 u2 u2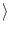 = 0.5 = 0.5 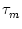 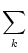 wk2 wk2 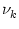 = 0.1 ; = 0.1 ; |
(5.83) |
cf. Section 5.5.2 for a different derivation. Let us now
increase all rates by a factor of a > 1 and multiply at the same time the
synaptic efficacies by a factor
1/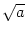 . Then both mean and variance of
the stochastic background input are the same as before, but the size wk
of the jumps is decreased; cf. Fig. 5.15B. In the limit of
a
. Then both mean and variance of
the stochastic background input are the same as before, but the size wk
of the jumps is decreased; cf. Fig. 5.15B. In the limit of
a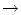
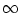 the jump process turns into a diffusion process and we arrive at
the stochastic model of Eq. (5.73). A systematic discussion of the
diffusion limit is the topic of the next subsection.
the jump process turns into a diffusion process and we arrive at
the stochastic model of Eq. (5.73). A systematic discussion of the
diffusion limit is the topic of the next subsection.
Since firing is driven by the fluctuations of the membrane potential, the
interspike intervals vary considerably; cf. Fig. 5.15. Balanced
excitatory and inhibitory spike input, could thus contribute to the large
variability of interspike intervals in cortical neurons
(Shadlen and Newsome, 1998; van Vreeswijk and Sompolinsky, 1996; Brunel and Hakim, 1999; Amit and Brunel, 1997a; Shadlen and Newsome, 1994; Tsodyks and Sejnowski, 1995); see
Section 5.6.
5.5.2 Diffusion limit (*)
In this section we analyze the model of stochastic spike arrival defined in
Eq. (5.74) and show how to map it to the diffusion
model defined in Eq. (5.73)
(Johannesma, 1968; Gluss, 1967; Capocelli and Ricciardi, 1971).
Suppose that the neuron has fired its last spike
at time 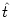 . Immediately after the firing the membrane potential was
reset to ur. Because of the stochastic spike arrival, we cannot predict the
membrane potential for t >
. Immediately after the firing the membrane potential was
reset to ur. Because of the stochastic spike arrival, we cannot predict the
membrane potential for t > 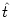 , but we can calculate its probability
density, p(u, t).
, but we can calculate its probability
density, p(u, t).
For the sake of simplicity, we set for the time being
Iext = 0 in Eq. (5.74). The input spikes at synapse k
are generated by a Poisson process and arrive stochastically with rate
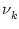 (t). The probability that no spike arrives in a short time interval
(t). The probability that no spike arrives in a short time interval
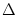 t is therefore
t is therefore
Prob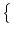 no spike in [t, t + no spike in [t, t + 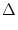 t] t] = 1 - = 1 - 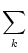 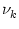 (t) (t) 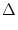 t . t . |
(5.84) |
If no spike arrives in
[t, t + 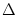 t], the membrane potential changes from
u(t) = u' to
u(t +
t], the membrane potential changes from
u(t) = u' to
u(t + 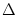 t) = u' exp(-
t) = u' exp(- 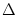 t/
t/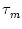 ). On the other
hand, if a spike arrives at synapse k, the membrane potential changes from
u' to
u' exp(-
). On the other
hand, if a spike arrives at synapse k, the membrane potential changes from
u' to
u' exp(- 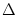 t/
t/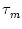 ) + wk. Given a value of u' at time
t, the probability density of finding a membrane potential u at time
t +
) + wk. Given a value of u' at time
t, the probability density of finding a membrane potential u at time
t + 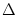 t is therefore given by
t is therefore given by
Ptrans(u, t + 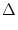 t| u', t) t| u', t) |
= |
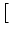 1 - 1 - 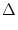 t t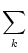 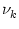 (t) (t)![$\displaystyle \big]$](img731.gif) 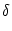  u - u' e- u - u' e-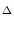 t/ t/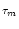  |
|
| |
|
+ 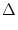 t t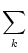 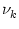 (t) (t)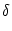 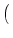 u - u' e- u - u' e-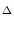 t/ t/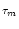 - wk - wk . . |
(5.85) |
We will refer to
Ptrans as the transition law. Since the membrane
potential is given by the differential equation (5.74) with input
spikes generated by a Poisson distribution, the evolution of the membrane
potential is a Markov Process (i.e., a process without memory) and can be
described by (van Kampen, 1992)
p(u, t + 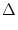 t) = t) = 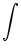 Ptrans(u, t + Ptrans(u, t + 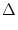 t| u', t) p(u', t) du' . t| u', t) p(u', t) du' . |
(5.86) |
We put Eq. (5.85) in (5.86). To perform the integration,
we have to recall the rules for 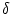 functions, viz.,
functions, viz.,
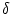 (a u) = a-1
(a u) = a-1 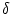 (u). The result of the integration is
(u). The result of the integration is
p(u, t + 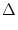 t) t) |
= |
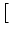 1 - 1 - 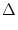 t t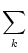 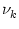 (t) (t)![$\displaystyle \big]$](img731.gif) e e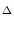 t/ t/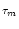 p p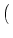 e e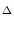 t/ t/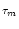 u, t u, t |
|
| |
|
+ 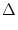 t t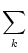 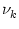 (t) e (t) e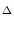 t/ t/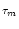 p p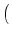 e e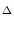 t/ t/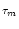 u - wk, t u - wk, t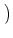 . . |
(5.87) |
Since 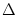 t is assumed to be small, we expand Eq. (5.87) about
t is assumed to be small, we expand Eq. (5.87) about
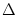 t = 0 and find to first order in
t = 0 and find to first order in 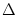 t
t
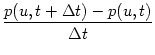 |
= |
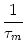 p(u, t) + p(u, t) + 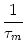 u u 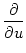 p(u, t) p(u, t) |
|
| |
|
+ 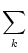 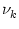 (t) (t) 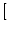 p(u - wk, t) - p(u, t) p(u - wk, t) - p(u, t)![$\displaystyle \left.\vphantom{ p(u-w_k,t) - p(u,t) }\right]$](img847.gif) . . |
(5.88) |
For
 t
t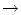 0, the left-hand side of Eq. (5.88) turns into a
partial derivative
0, the left-hand side of Eq. (5.88) turns into a
partial derivative
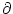 p(u, t)/
p(u, t)/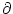 t. Furthermore, if the jump
amplitudes wk are small, we can expand the right-hand side of
Eq. (5.88) with respect to u about p(u, t):
t. Furthermore, if the jump
amplitudes wk are small, we can expand the right-hand side of
Eq. (5.88) with respect to u about p(u, t):
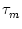 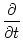 p(u, t) p(u, t) |
= |
- 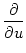  - u + - u + 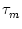 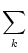 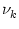 (t) wk (t) wk![$\displaystyle \left.\vphantom{ -u + \tau_m \sum_k \nu_k(t) \, w_k}\right]$](img850.gif) p(u, t) p(u, t) |
|
| |
|
+ 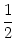 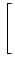 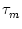 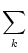 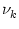 (t) wk2 (t) wk2![$\displaystyle \left.\vphantom{\tau_m \sum_k \nu_k(t) \, w_k^2}\right]$](img852.gif) 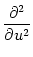 p(u, t) p(u, t) |
(5.89) |
where we have neglected terms of order wk3 and higher. The expansion in
wk is called the Kramers-Moyal expansion.
Eq. (5.89) is an example of a Fokker-Planck equation
(van Kampen, 1992), i.e., a partial differential
equation that describes the temporal evolution of a probability distribution.
The right-hand side of Eq. (5.89) has a clear interpretation:
The first term in rectangular brackets describes the systematic drift of the
membrane potential due to leakage (
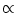 - u) and mean background
input (
- u) and mean background
input (
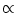
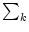
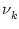 (t) wk). The second term in rectangular
brackets corresponds to a `diffusion constant' and accounts for the
fluctuations of the membrane potential. The Fokker-Planck
Eq. (5.89) is equivalent to the Langevin equation (5.73)
with
R I(t) =
(t) wk). The second term in rectangular
brackets corresponds to a `diffusion constant' and accounts for the
fluctuations of the membrane potential. The Fokker-Planck
Eq. (5.89) is equivalent to the Langevin equation (5.73)
with
R I(t) = 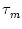
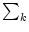
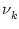 (t) wk and time-dependent noise
amplitude
(t) wk and time-dependent noise
amplitude
The specific process generated by the Langevin-equation (5.73) with constant noise amplitude 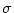 is called the Ornstein-Uhlenbeck process
(Uhlenbeck and Ornstein, 1930).
is called the Ornstein-Uhlenbeck process
(Uhlenbeck and Ornstein, 1930).
For the transition from Eq. (5.88) to (5.89) we have
suppressed higher-order terms in the expansion. The missing terms are
with
An = 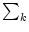
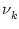 (t) wkn. What are the conditions that these
terms vanish? As in the example of Figs. 5.15A and B, we
consider a sequence of models where the size of the weights wk decreases so
that An
(t) wkn. What are the conditions that these
terms vanish? As in the example of Figs. 5.15A and B, we
consider a sequence of models where the size of the weights wk decreases so
that An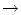 0 for n
0 for n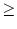 3 while the mean
3 while the mean
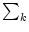
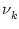 (t) wk and the
second moment
(t) wk and the
second moment
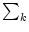
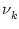 (t) wk2 remain constant. It turns out, that,
given both excitatory and inhibitory input, it is always possible to find an
appropriate sequence of models (Lansky, 1997,1984). For wk
(t) wk2 remain constant. It turns out, that,
given both excitatory and inhibitory input, it is always possible to find an
appropriate sequence of models (Lansky, 1997,1984). For wk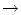 0, the
diffusion limit is attained and Eq. (5.89) is exact. For
excitatory input alone, however, such a sequence of models does not exist
(Plesser, 1999).
0, the
diffusion limit is attained and Eq. (5.89) is exact. For
excitatory input alone, however, such a sequence of models does not exist
(Plesser, 1999).
The Fokker-Planck equation (5.89) and the Langevin
equation (5.73) are equivalent descriptions of
drift and diffusion of the
membrane potential. Neither of these describe spike firing. To turn the
Langevin equation (5.73) into a sensible neuron model, we have to
incorporate a threshold condition. In the Fokker-Planck
equation (5.89), the firing threshold is
incorporated as a boundary condition
p(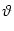 , t) , t) 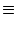 0 for all t . 0 for all t . |
(5.92) |
Before we continue the discussion of the diffusion model in the
presence of a threshold, let us study the solution of
Eq. (5.89) without threshold.
In the absence of a threshold (
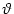
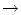
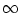 ), both the Langevin
equation (5.73) and the Fokker-Planck equation (5.89) can
be solved. Let us consider Eq. (5.73) for constant
), both the Langevin
equation (5.73) and the Fokker-Planck equation (5.89) can
be solved. Let us consider Eq. (5.73) for constant 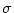 . At
t =
. At
t = 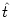 the membrane potential starts at a value u = ur = 0. Since
(5.73) is a linear equation, its solution is
the membrane potential starts at a value u = ur = 0. Since
(5.73) is a linear equation, its solution is
u(t|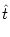 ) = ) = 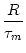 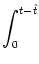 e-s/ e-s/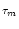 I(t - s) ds + I(t - s) ds + 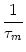 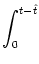 e-s/ e-s/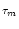 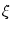 (t - s) ds (t - s) ds |
(5.93) |
Since
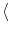
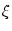 (t)
(t)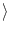 = 0, the expected trajectory of the membrane
potential is
= 0, the expected trajectory of the membrane
potential is
u0(t) = 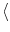 u(t| u(t|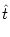 ) )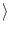 = = 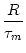 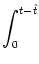 e-s/ e-s/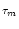 I(t - s) ds . I(t - s) ds . |
(5.94) |
In particular, for constant input current
I(t)  I0 we have
I0 we have
u0(t) = u  1 - e-(t- 1 - e-(t-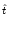 )/ )/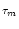 ![$\displaystyle \left.\vphantom{ 1 - e^{-(t-\hat{t})/\tau_m} }\right]$](img861.gif) |
(5.95) |
with
u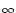 = R I0. Note that the expected trajectory is that of
the noiseless model.
= R I0. Note that the expected trajectory is that of
the noiseless model.
The fluctuations of the membrane potential have variance
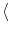
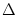 u2
u2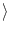 =
= 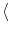 [u(t|
[u(t|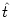 ) - u0(t)]2
) - u0(t)]2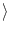 with u0(t) given by
Eq. (5.94). The variance can be evaluated with the help of
Eq. (5.93), i.e.,
with u0(t) given by
Eq. (5.94). The variance can be evaluated with the help of
Eq. (5.93), i.e.,
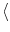 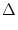 u2(t) u2(t)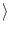 = = 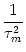 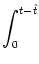 ds ds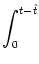 ds' e-s/ ds' e-s/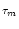 e-s'/ e-s'/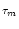 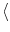 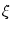 (t - s) (t - s) 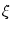 (t - s') (t - s')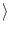 . . |
(5.96) |
We use
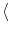
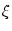 (t - s)
(t - s) 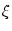 (t - s')
(t - s')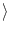 =
= 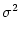
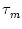
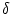 (s - s') and perform the
integration. The result is
(s - s') and perform the
integration. The result is
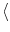 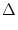 u2(t) u2(t)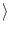 = = 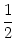 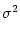  1 - e-2(t- 1 - e-2(t-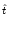 )/ )/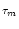 ![$\displaystyle \left.\vphantom{ 1 - e^{-2(t-\hat{t})/\tau_m} }\right]$](img865.gif) . . |
(5.97) |
Hence, noise causes the actual membrane trajectory to drift away from the
noiseless reference trajectory u0(t). The typical distance between the
actual trajectory and the mean trajectory approaches with time constant 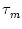 /2 a limiting value
/2 a limiting value
Figure 5.16:
In the absence of a threshold the membrane potential follows a Gaussian
distribution around the noise-free reference trajectory u0(t) (schematic
figure).
![\centerline{\includegraphics[width=60mm]{Fig-Gauss1a.eps}}](img869.gif) |
The solution of the Fokker-Planck equation (5.89) with initial
condition
p(u,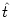 ) =
) = 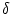 (u - ur) is a Gaussian with mean u0(t) and
variance
(u - ur) is a Gaussian with mean u0(t) and
variance
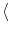
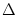 u2(t)
u2(t)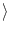 , i.e.,
, i.e.,
as can be verified by inserting Eq. (5.99) into
(5.89); see Fig. 5.16. In particular, the
stationary distribution that is approached in the limit of
t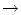
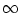 for
constant input I0 is
for
constant input I0 is
which describes a Gaussian distribution with mean
u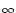 = R I0 and
variance
= R I0 and
variance
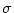 /
/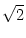 .
.
Let us consider a neuron that starts at time 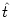 with a membrane potential
ur
and is driven for t >
with a membrane potential
ur
and is driven for t > 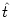 by a known input I(t).
Because of the diffusive noise generated by stochastic spike arrival,
we cannot predict the exact value of the neuronal membrane potential u(t)
at a later time t >
by a known input I(t).
Because of the diffusive noise generated by stochastic spike arrival,
we cannot predict the exact value of the neuronal membrane potential u(t)
at a later time t > 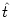 ,
but only the probability
that the membrane potential is in a certain interval [u0, u1].
Specifically, we have
,
but only the probability
that the membrane potential is in a certain interval [u0, u1].
Specifically, we have
Prob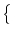 u0 < u(t) < u1 | u( u0 < u(t) < u1 | u(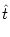 ) = ur ) = ur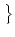 = = 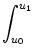 p(u, t) du p(u, t) du |
(5.101) |
where p(u, t) is the distribution of the membrane potential
at time t.
In the diffusion limit, p(u, t) can be found by solution of
the Fokker-Planck
equation Eq. (5.89) with initial condition
p(u,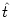 ) =
) = 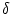 (u - ur) and boundary condition
p(
(u - ur) and boundary condition
p(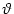 , t) = 0. At
any time t >
, t) = 0. At
any time t > 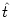 , the survivor function,
, the survivor function,
SI(t|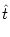 ) = ) = 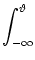 p(u, t) du , p(u, t) du , |
(5.102) |
is the probability that the membrane potential has not reached the
threshold. In view of Eq. (5.5), the input-dependent interval
distribution is therefore
PI(t|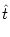 ) = - ) = - 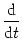 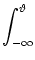 p(u, t) du . p(u, t) du . |
(5.103) |
We recall that
PI(t|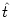 )
) 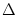 t for
t for
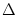 t
t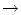 0 is the
probability that a neuron fires its next spike between t and
t +
0 is the
probability that a neuron fires its next spike between t and
t + 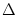 t
given a spike at
t
given a spike at 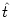 and input I. In the context of noisy
integrate-and-fire neurons
PI(t|
and input I. In the context of noisy
integrate-and-fire neurons
PI(t|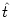 ) is called the distribution of
`first passage times'. The name is motivated by the
fact, that firing occurs when the membrane potential crosses
) is called the distribution of
`first passage times'. The name is motivated by the
fact, that firing occurs when the membrane potential crosses 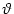 for
the first time. Unfortunately, no general solution is known for the first
passage time problem of the Ornstein-Uhlenbeck process. For constant input
I(t) = I0, however, it is at least possible to give a moment expansion
of the first passage time distribution. In particular, the mean of the first
passage time can be calculated in closed form.
for
the first time. Unfortunately, no general solution is known for the first
passage time problem of the Ornstein-Uhlenbeck process. For constant input
I(t) = I0, however, it is at least possible to give a moment expansion
of the first passage time distribution. In particular, the mean of the first
passage time can be calculated in closed form.
For constant input I0 the mean interspike interval is
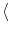 s
s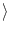 =
= 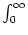 s PI0(s| 0)ds =
s PI0(s| 0)ds = 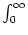 s P0(s)ds; cf.
Eq. (5.21). For the diffusion model Eq. (5.73) with threshold
s P0(s)ds; cf.
Eq. (5.21). For the diffusion model Eq. (5.73) with threshold
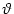 reset potential ur, and membrane time constant
reset potential ur, and membrane time constant 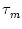 , the
mean interval is
, the
mean interval is
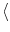 s s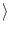 = = 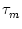 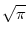 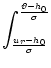 du exp du exp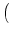 u2 u2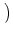 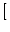 1 + erf(u) 1 + erf(u)![$\displaystyle \left.\vphantom{1+ {\rm erf}(u)}\right]$](img889.gif) , , |
(5.104) |
where
h0 = R I0 is the input potential caused by the constant current
I0 (Johannesma, 1968). This expression can be derived by several
methods; for reviews see, e.g., (Tuckwell, 1988; van Kampen, 1992). We will return
to Eq. (5.104) in Chapter 6.2.1 in
the context of populations of spiking neurons.
Figure 5.17:
Without a threshold, several trajectories can reach at time t the same
value
u = 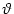 from above or below.
from above or below.
![\centerline{\includegraphics[height=35mm,width=60mm]{Fig-Schroedinger.eps}}](img890.gif) |
We have seen that, in the absence of a threshold, the Fokker-Planck Equation
(5.89) can be solved; cf. Eq. (5.99). The transition
probability from an arbitrary starting value u' at time t' to a new value
u at time t is
Ptrans(u, t| u', t') = 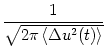 exp exp![$\displaystyle \left\{\vphantom{ - {[u - u_0(t)]^2 \over 2 \,\langle \Delta u^2(t) \rangle} }\right.$](img891.gif) - - ![$\displaystyle {[u - u_0(t)]^2 \over 2 \,\langle \Delta u^2(t) \rangle}$](img892.gif) ![$\displaystyle \left.\vphantom{ - {[u - u_0(t)]^2 \over 2 \,\langle \Delta u^2(t) \rangle} }\right\}$](img893.gif) |
(5.105) |
with
| u0(t) |
= |
u' e-(t-t')/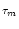 + + 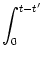 e-s'/ e-s'/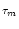 I(t - s') ds I(t - s') ds |
(5.106) |
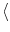 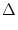 u2(t) u2(t)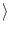 |
= |
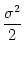  1 - e-2 (t-s)/ 1 - e-2 (t-s)/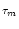 ![$\displaystyle \left.\vphantom{ 1 - e^{-2\,(t-s)/\tau_m} }\right]$](img897.gif) . . |
(5.107) |
A method due to Schrödinger uses the solution of the unbounded problem in
order to calculate the input-dependent interval distribution
PI(t|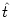 )
of the diffusion model with threshold
(Schrödinger, 1915; Plesser and Tanaka, 1997; Burkitt and Clark, 1999). The idea of the solution method is
illustrated in Fig. 5.17. Because of the Markov property,
the probability density to cross the threshold (not necessarily for the first
time) at a time t, is equal to the probability to cross it for the first
time at t' < t and to return back to
)
of the diffusion model with threshold
(Schrödinger, 1915; Plesser and Tanaka, 1997; Burkitt and Clark, 1999). The idea of the solution method is
illustrated in Fig. 5.17. Because of the Markov property,
the probability density to cross the threshold (not necessarily for the first
time) at a time t, is equal to the probability to cross it for the first
time at t' < t and to return back to 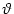 at time t, that is,
at time t, that is,
Ptrans(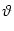 , t| ur, , t| ur,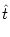 ) = ) = 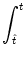 PI(t'| PI(t'|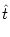 ) Ptrans( ) Ptrans(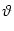 , t| , t|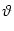 , t') dt' . , t') dt' . |
(5.108) |
This integral equation can be solved numerically for the distribution
PI(t'|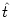 ) for arbitrary input current I(t) (Plesser, 2000).
An example is shown in Fig. 5.18.
) for arbitrary input current I(t) (Plesser, 2000).
An example is shown in Fig. 5.18.
Figure 5.18:
A time-dependent input current I(t) generates a noise-free membrane
potential u0(t) shown in the lower part of the figure. In the presence
of diffusive noise, spikes can be triggered although the reference
trajectory stays below the threshold (dashed line). This gives rise to an
input-dependent interval distribution PI(t| 0) shown in the upper panel.
Taken from (Plesser and Gerstner, 2000).
![\centerline{\includegraphics[width=80mm]{Plesser2a-single.eps}} \centerline{\includegraphics[width=80mm]{Plesser2b.eps}}\par\vspace{0mm}](img898.gif) |





Next: 5.6 The subthreshold regime
Up: 5. Noise in Spiking
Previous: 5.4 Slow noise in
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![]() du/dt = - u + R I(t) where
du/dt = - u + R I(t) where ![]() is the membrane time constant, R the input resistance, and I the input
current. The standard procedure of implementing noise in such a differential
equation is to add a `noise term',
is the membrane time constant, R the input resistance, and I the input
current. The standard procedure of implementing noise in such a differential
equation is to add a `noise term', ![]() (t), on the right-hand side. The noise
term
(t), on the right-hand side. The noise
term ![]() is a stochastic process called `Gaussian white noise' characterized
by its expectation value,
is a stochastic process called `Gaussian white noise' characterized
by its expectation value,
![]()
![]() (t)
(t)![]() = 0, and the autocorrelation
= 0, and the autocorrelation
![]() ; cf.
Fig. 5.12. We will refer to Eq. (5.73) as the Langevin
equation of the noisy integrate-and-fire model. The analysis of
Eq. (5.73) in the presence of the threshold
; cf.
Fig. 5.12. We will refer to Eq. (5.73) as the Langevin
equation of the noisy integrate-and-fire model. The analysis of
Eq. (5.73) in the presence of the threshold ![]() is the topic of
this section. Before we start with the discussion of Eq. (5.73), we
indicate how the noise term
is the topic of
this section. Before we start with the discussion of Eq. (5.73), we
indicate how the noise term ![]() (t) can be motivated by stochastic spike
arrival.
(t) can be motivated by stochastic spike
arrival.
![\centerline{\includegraphics[width=60mm]{noise-diff-mod.eps}}](img812.gif)
![\centerline{\includegraphics[width=100mm]{spike-input2a.eps}}](img813.gif)
![]() u(t) = wj
u(t) = wj![]() (t - tj(f)) with
(t - tj(f)) with
![]() (s) = e-s/
(s) = e-s/![]()
![]() (s),
i.e., the potential jumps upon spike arrival by an amount wj and decays
exponentially thereafter. It is straightforward to generalize the model so as
to include a synaptic time constant and work with arbitrary postsynaptic
potentials
(s),
i.e., the potential jumps upon spike arrival by an amount wj and decays
exponentially thereafter. It is straightforward to generalize the model so as
to include a synaptic time constant and work with arbitrary postsynaptic
potentials
![]() (s) that are generated by stochastic spike arrival; cf. Fig. 5.14A.
(s) that are generated by stochastic spike arrival; cf. Fig. 5.14A.
![]() . Each input spike evokes a
postsynaptic potential
w0
. Each input spike evokes a
postsynaptic potential
w0 ![]() (s). The input statistics is assumed
to be Poisson, i.e., firing times are independent. Thus, the input spike
train,
(s). The input statistics is assumed
to be Poisson, i.e., firing times are independent. Thus, the input spike
train,
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[height=35mm,width...
...udegraphics[width=60mm]{pout.dat.spikes-all.eps}
\end{minipage} \vspace{-35mm}](img823.gif)
![]() u(t)
u(t)![]() and the
variance
and the
variance
![]()
![]() u2
u2![]() =
= ![]() [u(t) - u0]2
[u(t) - u0]2![]() . Using
Eqs. (5.76) and (5.77) we find
. Using
Eqs. (5.76) and (5.77) we find
![]() (s) = e-s/
(s) = e-s/![]() . The result is
. The result is
![]() = 10ms receives input from 100 excitatory
neurons (
wk = + 0.1) and 100 inhibitory neurons (
wk = - 0.1). Each
background neuron k fires at a rate of
= 10ms receives input from 100 excitatory
neurons (
wk = + 0.1) and 100 inhibitory neurons (
wk = - 0.1). Each
background neuron k fires at a rate of ![]() = 10Hz. Thus, in each
millisecond, the neuron receives on average one excitatory and one inhibitory
input spike. Each spike leads to a jump of the membrane potential of ±0.1. The trajectory of the membrane potential is therefore similar to that
of a random walk; cf. Fig. 5.15A. If, in
addition, a constant stimulus
Iext = I0 > 0 is applied so that the
mean membrane potential (in the absence of the background spikes) is just
below threshold, then the presence of random background spikes may drive u
towards the firing threshold. Whenever
u
= 10Hz. Thus, in each
millisecond, the neuron receives on average one excitatory and one inhibitory
input spike. Each spike leads to a jump of the membrane potential of ±0.1. The trajectory of the membrane potential is therefore similar to that
of a random walk; cf. Fig. 5.15A. If, in
addition, a constant stimulus
Iext = I0 > 0 is applied so that the
mean membrane potential (in the absence of the background spikes) is just
below threshold, then the presence of random background spikes may drive u
towards the firing threshold. Whenever
u![]()
![]() , the membrane
potential is reset to ur = 0.
, the membrane
potential is reset to ur = 0.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[height=35mm,width...
...ludegraphics[height=35mm,width=60mm]{pout.dat.IF-of-t-diff2.eps}
\end{minipage}](img828.gif)
![]() wk
wk ![]() = 0. Using the same arguments as in the previous
example, we can convince ourselves that the stochastic arrival of background
spikes generates fluctuations of the voltage with variance
= 0. Using the same arguments as in the previous
example, we can convince ourselves that the stochastic arrival of background
spikes generates fluctuations of the voltage with variance
![]() . Immediately after the firing the membrane potential was
reset to ur. Because of the stochastic spike arrival, we cannot predict the
membrane potential for t >
. Immediately after the firing the membrane potential was
reset to ur. Because of the stochastic spike arrival, we cannot predict the
membrane potential for t > ![]() , but we can calculate its probability
density, p(u, t).
, but we can calculate its probability
density, p(u, t).
![]() (t). The probability that no spike arrives in a short time interval
(t). The probability that no spike arrives in a short time interval
![]() t is therefore
t is therefore
![]()
![]()
![]() ), both the Langevin
equation (5.73) and the Fokker-Planck equation (5.89) can
be solved. Let us consider Eq. (5.73) for constant
), both the Langevin
equation (5.73) and the Fokker-Planck equation (5.89) can
be solved. Let us consider Eq. (5.73) for constant ![]() . At
t =
. At
t = ![]() the membrane potential starts at a value u = ur = 0. Since
(5.73) is a linear equation, its solution is
the membrane potential starts at a value u = ur = 0. Since
(5.73) is a linear equation, its solution is
![]()
![]() u2
u2![]() =
= ![]() [u(t|
[u(t|![]() ) - u0(t)]2
) - u0(t)]2![]() with u0(t) given by
Eq. (5.94). The variance can be evaluated with the help of
Eq. (5.93), i.e.,
with u0(t) given by
Eq. (5.94). The variance can be evaluated with the help of
Eq. (5.93), i.e.,
![\centerline{\includegraphics[width=60mm]{Fig-Gauss1a.eps}}](img869.gif)
![]() ) =
) = ![]() (u - ur) is a Gaussian with mean u0(t) and
variance
(u - ur) is a Gaussian with mean u0(t) and
variance
![]()
![]() u2(t)
u2(t)![]() , i.e.,
, i.e.,
![]() with a membrane potential
ur
and is driven for t >
with a membrane potential
ur
and is driven for t > ![]() by a known input I(t).
Because of the diffusive noise generated by stochastic spike arrival,
we cannot predict the exact value of the neuronal membrane potential u(t)
at a later time t >
by a known input I(t).
Because of the diffusive noise generated by stochastic spike arrival,
we cannot predict the exact value of the neuronal membrane potential u(t)
at a later time t > ![]() ,
but only the probability
that the membrane potential is in a certain interval [u0, u1].
Specifically, we have
,
but only the probability
that the membrane potential is in a certain interval [u0, u1].
Specifically, we have
![]() s
s![]() =
= ![]() s PI0(s| 0)ds =
s PI0(s| 0)ds = ![]() s P0(s)ds; cf.
Eq. (5.21). For the diffusion model Eq. (5.73) with threshold
s P0(s)ds; cf.
Eq. (5.21). For the diffusion model Eq. (5.73) with threshold
![]() reset potential ur, and membrane time constant
reset potential ur, and membrane time constant ![]() , the
mean interval is
, the
mean interval is
![\centerline{\includegraphics[height=35mm,width=60mm]{Fig-Schroedinger.eps}}](img890.gif)
![\centerline{\includegraphics[width=80mm]{Plesser2a-single.eps}} \centerline{\includegraphics[width=80mm]{Plesser2b.eps}}\par\vspace{0mm}](img898.gif)