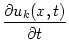 = - uk(x, t) + = - uk(x, t) + |
(9.35) |
Up to now we have treated only a single sheet of neurons that were all of the same type. Excitatory and inhibitory couplings were lumped together in a single function w that gave the `average' coupling strength of two neurons as a function of their distance. `Real' neurons, however, are either excitatory or inhibitory, because they can use only one type of neurotransmitter (Dale's law). A coupling function that yields both positive and negative values for the synaptic couplings is therefore not realistic.
We can easily extend the previous model so as to account for different types of neuron or for several separate layers of neuronal tissue. To this end we embellish the variable u for the average membrane potential with an additional index k, k = 1,..., n, that denotes the type of the neuron or its layer. Furthermore, we introduce coupling functions wkl(x, x') that describe the coupling strength of a neuron from layer l at position x' to a neuron located in layer k and position x. In analogy to Eq. (9.4) the field equations will be defined as
| w11 |
(9.36) |
As before we start our analysis of the field equations by looking for homogeneous solutions. Substitution of uk(x, t) = uk(t) into Eq. (9.36) yields
We can gain an intuitive understanding of the underlying mechanism by means of
phase-plane analysis - a tool which we have already encountered in
Chapter 3. Figure 9.8 shows the flow-field and null-clines of
Eq. (9.39) with ![]() = 1,
= 1, ![]() = 5,
= 5,
![]() =
= ![]() = 2,
= 2,
![]() = - 1, and
= - 1, and
![]() = 0. The gain function has a standard form, i.e.,
g(u) = {1 + exp[
= 0. The gain function has a standard form, i.e.,
g(u) = {1 + exp[![]() (u -
(u - ![]() )]}-1 with
)]}-1 with ![]() = 5 and
= 5 and ![]() = 1.
= 1.
For zero external input Eq. (9.39) has only a single stable fixed point close to (u1, u2) = (0, 0). This fixed point is attractive so that the system will return immediately to its resting position after a small perturbation; cf. Fig. 9.8A. If, for example, the external input to the excitatory layer is gradually increased, the behavior of the systems may change rather dramatically. Figure 9.8B shows that for Iext, 1 = 0.3 the system does not return immediately to its resting state after an initial perturbation but takes a large detour through phase space. In doing so, the activity of the network transiently increases before it finally settles down again at its resting point; cf. Fig. 9.8B. This behavior is qualitatively similar to the triggering of an action potential in a two-dimensional neuron model (cf. Chapter 3), though the interpretation in the present case is different. We will refer to this state of the network as an excitable state.
![\begin{minipage}{0.32\textwidth}
{\bf A} ($I^{\text{ext},1}=0$)
\par\includegra...
...xt},1}=0.5$)
\par\includegraphics[width=\textwidth]{bif_3.ps.gz}
\end{minipage}](img1484.gif) |
If the strength of the input is further increased the system undergoes a series of bifurcations so that the attractive (0, 0)-fixed point will finally be replaced by an unstable fixed point near (1, 1) which is surrounded by a stable limit cycle; cf. Fig. 9.8C. This corresponds to an oscillatory state where excitatory and inhibitory neurons get activated alternatingly. Provided that the homogenous solution is stable with respect to inhomogeneous perturbations global network oscillations can be observed; cf. Fig. 9.9.
![\begin{minipage}[t]{0.48\textwidth}
{\bf A}
\par\includegraphics[width=\textwid...
...ce{5mm}
\includegraphics[width=\textwidth]{oscillation_2.ps.gz}
\end{minipage}](img1485.gif) |
Traveling waves are a well-known phenomenon and occur in a broad class of different systems that have collectively been termed excitable media. A large class of examples for these systems is provided by reaction-diffusion systems where the interplay of a chemical reaction with the diffusion of its reactants results in an often surprisingly rich variety of dynamical behavior. All these systems share a common property, namely `excitability'. In the absence of an external input the behavior of the system is characterized by a stable fixed point, its resting state. Additional input, however, can evoke a spike-like rise in the activation of the system. Due to lateral interactions within the system such a pulse of activity can propagate through the medium without changing its form and thus forming a traveling wave.
In the previous section we have seen that the present system consisting of two separate layers of excitatory and inhibitory neurons can indeed exhibit an excitable state; cf. Fig. 9.8B. It is thus natural to look for a special solution of the field equations (9.36) in the form of a traveling wave. To this end we make an ansatz,
| uk(x, t) = |
(9.39) |
| 0 = - |
(9.42) |
Finding a solution of the integro-differential equation (![]() ) analytically is obviously a hard problem unless a particularly
simple form of the gain function g is employed. One possibility is
to use a step function such as
) analytically is obviously a hard problem unless a particularly
simple form of the gain function g is employed. One possibility is
to use a step function such as
g(u) = 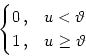 |
(9.43) |
![\begin{minipage}[t]{0.48\textwidth}
{\bf A}
\par\includegraphics[width=\textwid...
...ar\vspace{5mm}
\includegraphics[width=\textwidth]{wave_3.ps.gz}
\end{minipage}](img1498.gif) |
Figure 9.10 shows an example of a traveling wave
in a network with excitatory (layer 1, ![]() = 1) and
inhibitory (layer 2,
= 1) and
inhibitory (layer 2, ![]() = 5) neurons. The coupling functions are
bell-shaped [cf. Eq. (9.38)] with
= 5) neurons. The coupling functions are
bell-shaped [cf. Eq. (9.38)] with
![]() =
= ![]() =
= ![]() = 1 and
= 1 and
![]() =
= ![]() = 2,
= 2,
![]() = - 1, and
= - 1, and
![]() = 0, as before. The excitatory neurons receive tonic
input
Iext, 1 = 0.3 in order to reach the excitable state
(cf. Fig. 9.8B). A short pulse of additional excitatory
input suffices to trigger a pair of pulses of activity that travel in
opposite direction through the medium.
= 0, as before. The excitatory neurons receive tonic
input
Iext, 1 = 0.3 in order to reach the excitable state
(cf. Fig. 9.8B). A short pulse of additional excitatory
input suffices to trigger a pair of pulses of activity that travel in
opposite direction through the medium.
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.