




Next: 9.2 Dynamic patterns of
Up: 9. Spatially Structured Networks
Previous: 9. Spatially Structured Networks
Subsections
9.1 Stationary patterns of neuronal activity
We start with a generic example of pattern formation in a neural network with
`Mexican-hat' shaped lateral coupling, i.e., local excitation and long-range
inhibition. In order to keep the notation as simple as possible, we will use
the field equation derived in Chapter 6;
cf. Eq. (6.129). As
we have seen in Fig. 6.8, this equation neglects rapid
transients and oscillations that could be captured by the full integral
equations. On the other hand, in the limit of high noise and short
refractoriness the approximation of population dynamics by differential
equations is good; cf. Chapter 7. Exact solutions in the
low-noise limit will be discussed in
Section 9.3.
Consider a single sheet of densely packed neurons. We assume that all neurons
are alike and that the connectivity is homogeneous and isotropic, i.e., that
the coupling strength of two neurons is a function of their distance only. We
loosely define a quantity u(x, t) as the average membrane potential of the
group of neurons located at position x at time t. We have seen in
Chapter 6 that in the stationary state the `activity' of
a population of neurons is strictly given by the single-neuron gain function
A0(x) = g[u0(x)]; cf. Fig. 9.1. If we assume
that changes of the input potential are slow enough so that the population
always remains in a state of incoherent firing, then we can set
| A(x, t) = g[u(x, t)] , |
(9.1) |
even for time-dependent situations. According to Eq. (9.1), the
activity A(x, t) of the population around location x is a function of the
potential at that location.
The synaptic input current to a given neuron depends on the level of activity
of its presynaptic neurons and on the strength of the synaptic couplings. We
assume that the amplitude of the input current is simply the presynaptic
activity scaled by the average coupling strength of these neurons. The total
input current
Isyn(x, t) to a neuron at position x is therefore
Isyn(x, t) = 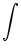 dy w dy w  x - y x - y  A(y, t) . A(y, t) . |
(9.2) |
Here, w is the average coupling strength of two neurons as a
function of their distance. We consider a
connectivity pattern, that is excitatory for proximal neurons and
predominantly inhibitory for distal neurons. Figure ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) B shows the typical `Mexican-hat shape' of the
corresponding coupling function.
Eq. (9.2) assumes that synaptic interaction
is instantaneous. In a more detailed model we could
include the axonal transmission delay and synaptic time constants.
In that case, A(y, t) on the right-hand side of Eq. (9.2)
should be replaced by
B shows the typical `Mexican-hat shape' of the
corresponding coupling function.
Eq. (9.2) assumes that synaptic interaction
is instantaneous. In a more detailed model we could
include the axonal transmission delay and synaptic time constants.
In that case, A(y, t) on the right-hand side of Eq. (9.2)
should be replaced by
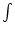
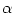 (s) A(y, t - s) ds where
(s) A(y, t - s) ds where
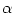 (s) is the temporal interaction kernel.
(s) is the temporal interaction kernel.
Figure 9.1:
A. Generic form of the sigmoidal gain function
g of graded response neurons that describes the relation between the
potential u and the `activity' of the neural population. B. Typical `Mexican hat'-shaped function that is used here as an ansatz
for the coupling w of two neurons as a function of their distance
x.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...\bf B}
\par\includegraphics[width=\textwidth]{mexican_hat.ps.gz}
\end{minipage}](img1399.gif) |
In order to complete the definition
of the model, we need to specify a relation between the input current and the
resulting membrane potential. In order to keep things simple we treat
each neuron as a leaky integrator. The input potential is thus
given by a differential equation of the form
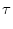 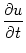 = - u + Isyn + Iext , = - u + Isyn + Iext , |
(9.3) |
with 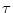 being the time constant of the integrator and
Iext an additional external input. If we put
things together we obtain the field equation
being the time constant of the integrator and
Iext an additional external input. If we put
things together we obtain the field equation
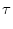 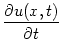 = - u(x, t) + = - u(x, t) + 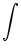 dy w dy w  x - y x - y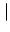  g[u(y, t)] + Iext(x, t) ; g[u(y, t)] + Iext(x, t) ; |
(9.4) |
cf. Amari (1977b); Feldman and Cowan (1975); Wilson and Cowan (1973); Kishimoto and Amari (1979).
This is a nonlinear integro-differential equation for the average
membrane potential u(x, t).
9.1.1 Homogeneous solutions
Although we have kept the above model as simple as possible, the field
equation (9.4) is complicated enough to prevent comprehensive
analytical treatment. We therefore start our investigation by looking for a
special type of solution, i.e., a solution that is uniform over space, but not
necessarily constant over time. We call this the homogenous solution and
write
u(x, t)  u(t). We expect that a homogenous solution exists if
the external input is homogeneous as well, i.e., if
Iext(x, t)
u(t). We expect that a homogenous solution exists if
the external input is homogeneous as well, i.e., if
Iext(x, t)  Iext(t).
Iext(t).
Substitution of the ansatz
u(x, t) 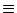 u(t) into Eq. (9.4)
yields
u(t) into Eq. (9.4)
yields
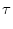 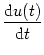 = - u(t) + = - u(t) + 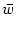 g[u(t)] + Iext(t) . g[u(t)] + Iext(t) . |
(9.5) |
with
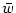 =
= 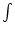 dy w
dy w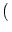
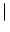 y
y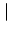
 . This is a nonlinear ordinary differential equation for the average
membrane potential u(t). We note that the equation for the homogeneous
solution is identical to that of a single population without spatial
structure; cf. Eq. (6.87) in Chapter 6.3.
. This is a nonlinear ordinary differential equation for the average
membrane potential u(t). We note that the equation for the homogeneous
solution is identical to that of a single population without spatial
structure; cf. Eq. (6.87) in Chapter 6.3.
The fixed points of the above equation with
Iext = 0 are of
particular interest because they correspond to a resting state of the network.
More generally, we search for stationary solutions for a given constant
external input
Iext(x, t) 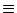 Iext. The fixed
points of Eq. (9.5) are solutions of
Iext. The fixed
points of Eq. (9.5) are solutions of
g(u) = 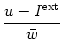 , , |
(9.6) |
which is represented graphically in Fig. 9.2. Depending
on the strength of the external input three qualitatively different
situations can be observed. For low external stimulation there is a single
fixed point at a very low level of neuronal activity. This corresponds
to a quiescent state where the activity of the whole network has
ceased. Large stimulation results in a fixed point at an almost
saturated level of activity which corresponds to a state where all
neurons are firing at their maximum rate. Intermediate values of
external stimulation, however, may result in a situation with more
than one fixed point. Depending on the shape of the output function
and the mean synaptic coupling strength 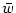 three fixed points
may appear. Two of them correspond to the quiescent and the highly
activated state, respectively, which are separated by the third fixed
point at an intermediate level of activity.
three fixed points
may appear. Two of them correspond to the quiescent and the highly
activated state, respectively, which are separated by the third fixed
point at an intermediate level of activity.
Figure 9.2:
Graphical representation of the fixed-point equation
(9.6). The solid line corresponds to the neuronal
gain function g(u) and the dashed lines to
(u - Iext)/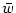 for different amounts of
external stimulation
Iext. Depending on the amount of
Iext there is either a stable fixed point at low
activity (leftmost black dot), a stable fixed point at high
activity (rightmost black dot), or a bistable situation with
stable fixed points (black dots on center line) separated by an
unstable fixed point at intermediate level of activity (small
circle).
for different amounts of
external stimulation
Iext. Depending on the amount of
Iext there is either a stable fixed point at low
activity (leftmost black dot), a stable fixed point at high
activity (rightmost black dot), or a bistable situation with
stable fixed points (black dots on center line) separated by an
unstable fixed point at intermediate level of activity (small
circle).
![\centerline{\includegraphics[width=0.45\textwidth]{fixed_points.ps.gz}}](img1410.gif) |
Any potential physical relevance of fixed points clearly depends on
their stability. Stability under the dynamics defined by the ordinary
differential equation Eq. (9.5) is readily checked using
standard analysis. Stability requires that at the intersection
g'(u) < 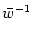 . . |
(9.7) |
Thus all fixed points corresponding to quiescent or highly activated states
are stable whereas the middle fixed point in case of multiple solutions is
unstable; cf. Fig. 9.2. This, however, is only half of the
truth because Eq. (9.5) only describes homogeneous
solutions. Therefore, it may
well be that the solutions are stable with respect to Eq. (9.5), but unstable with respect to inhomogeneous perturbations,
i.e., to perturbations that do not have the same amplitude everywhere in the
net.
In the following we will perform a linear stability analysis of the
homogeneous solutions found in the previous section. To this end we study the
field equation (9.4) and consider small perturbations about
the homogeneous solution. A linearization of the field equation will lead to
a linear differential equation for the amplitude of the perturbation. The
homogeneous solution is said to be stable if the amplitude of every small
perturbation is decreasing whatever its shape.
Suppose
u(x, t) 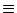 u0 is a homogeneous solution of Eq. (9.4),
i.e.,
u0 is a homogeneous solution of Eq. (9.4),
i.e.,
0 = - u0 + 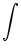 dy w dy w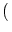 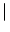 x - y x - y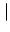  g[u0] + Iext . g[u0] + Iext . |
(9.8) |
Consider a small perturbation
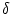 u(x, t) with initial amplitude
u(x, t) with initial amplitude

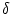 u(x, 0)
u(x, 0)
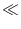 1. We substitute
u(x, t) = u0 +
1. We substitute
u(x, t) = u0 + 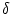 u(x, t) in
Eq. (9.4) and linearize with respect to
u(x, t) in
Eq. (9.4) and linearize with respect to 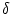 u,
u,
Here, a prime denotes the derivative with respect to the argument. Zero-order
terms cancel each other because of Eq. (9.8). If we collect all terms
linear in 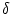 u we find
u we find
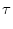 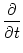 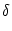 u(x, t) = - u(x, t) = - 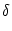 u(x, t) + g'(u0) u(x, t) + g'(u0) 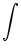 dy w(| x - y|) dy w(| x - y|) 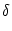 u(y, t) ; u(y, t) ; |
(9.9) |
We make two important observations. First, Eq. (9.10) is linear in the perturbations 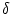 u - simply because we have neglected
terms of order
(
u - simply because we have neglected
terms of order
(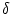 u)n with n
u)n with n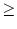 2. Second, the coupling between
neurons at locations x and y is mediated by the coupling kernel
w
2. Second, the coupling between
neurons at locations x and y is mediated by the coupling kernel
w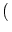
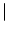 x - y
x - y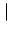
 that depends only on the distance | x - y|.
If we apply a Fourier transform over the spatial coordinates, the convolution
integral turns into a simple multiplication. It suffices therefore to discuss
a single (spatial) Fourier component of
that depends only on the distance | x - y|.
If we apply a Fourier transform over the spatial coordinates, the convolution
integral turns into a simple multiplication. It suffices therefore to discuss
a single (spatial) Fourier component of
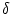 u(x, t). Any specific initial
form of
u(x, t). Any specific initial
form of
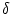 u(x, 0) can be created from its Fourier components by virtue
of the superposition principle. We can therefore proceed without loss of
generality by considering a single Fourier component, viz.,
u(x, 0) can be created from its Fourier components by virtue
of the superposition principle. We can therefore proceed without loss of
generality by considering a single Fourier component, viz.,
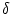 u(x, t) = c(t) ei k x. If we substitute this ansatz in Eq. (9.10)
we obtain
u(x, t) = c(t) ei k x. If we substitute this ansatz in Eq. (9.10)
we obtain
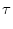 c'(t) c'(t) |
= - c(t) 1 - g'(u0) 1 - g'(u0) 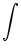 dy w(| x - y|) ei k (y-x) dy w(| x - y|) ei k (y-x)![$\displaystyle \left.\vphantom{ 1 - g'(u_0) \, \int \!\! {\text{d}}y \; w(\vert x-y\vert) \, {\text{e}}^{i\,k \, (y-x)} }\right]$](img1418.gif) |
|
| |
= - c(t) 1 - g'(u0) 1 - g'(u0) 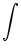 dz w(| z|) ei k z dz w(| z|) ei k z![$\displaystyle \left.\vphantom{ 1 - g'(u_0) \, \int \!\! {\text{d}}z \; w(\vert z\vert) \, {\text{e}}^{i\,k \, z} }\right]$](img1420.gif) , , |
(9.10) |
which is a linear differential equation for the amplitude c
of a perturbation with wave number k. This equation is solved by
c(t) = c(0) e-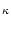 (k) t , (k) t , |
(9.11) |
with
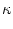 (k) = 1 - g'(u0) (k) = 1 - g'(u0) 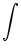 dz w(| z|) ei k z . dz w(| z|) ei k z . |
(9.12) |
Stability of the solution u0 with respect to a perturbation with wave
number k depends on the sign of the real part of 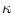 (k). Note that -
quite intuitively - only two quantities enter this expression, namely the
slope of the activation function evaluated at u0 and the Fourier transform
of the coupling function w evaluated at k. If the real part of the
Fourier transform of w stays below 1/g'(u0), then u0 is stable.
Note that Eqs. (9.12) and (9.13) are
valid for an arbitrary coupling function w(| x - y|). In the following two
examples we illustrate the typical behavior for two specific choices of the
lateral coupling.
(k). Note that -
quite intuitively - only two quantities enter this expression, namely the
slope of the activation function evaluated at u0 and the Fourier transform
of the coupling function w evaluated at k. If the real part of the
Fourier transform of w stays below 1/g'(u0), then u0 is stable.
Note that Eqs. (9.12) and (9.13) are
valid for an arbitrary coupling function w(| x - y|). In the following two
examples we illustrate the typical behavior for two specific choices of the
lateral coupling.
We now apply Eq. (9.13) to a network with purely excitatory
couplings. For the sake of simplicity we take a one-dimensional sheet of
neurons and assume that the coupling function is bell-shaped, i.e.,
w(x) = 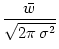 e-x2/(2 e-x2/(2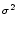 ) , ) , |
(9.13) |
with the mean strength
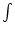 dx w(x) =
dx w(x) = 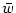 and
characteristic length scale
and
characteristic length scale 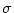 . The Fourier transform of w is
. The Fourier transform of w is
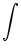 dx w(x) ei k x = dx w(x) ei k x = 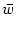 e-k2 e-k2 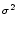 /2 , /2 , |
(9.14) |
with maximum 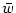 at k = 0. According to Eq. (9.13) a
homogeneous solution u0 is stable if
1 -
at k = 0. According to Eq. (9.13) a
homogeneous solution u0 is stable if
1 - 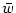 g'(u0) > 0. This is precisely the result obtained by the simple stability analysis
based on the homogeneous field equation;
cf. Eq. (9.7). This result indicates that no
particularly interesting phenomena will arise in networks with purely
excitatory coupling.
g'(u0) > 0. This is precisely the result obtained by the simple stability analysis
based on the homogeneous field equation;
cf. Eq. (9.7). This result indicates that no
particularly interesting phenomena will arise in networks with purely
excitatory coupling.
A more interesting example is provided by a combination of excitatory and
inhibitory coupling described by the difference of two bell-shaped functions
with different width. For the sake of simplicity we will again consider a
one-dimensional sheet of neurons. For the lateral coupling we take
w(x) = 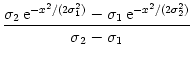 , , |
(9.15) |
with
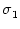 <
< 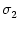 . The normalization of the coupling function has been
chosen so that w(0) = 1 and
. The normalization of the coupling function has been
chosen so that w(0) = 1 and
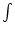 dx w(x) =
dx w(x) = 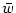 = 0;
cf Fig. 9.3A.
= 0;
cf Fig. 9.3A.
Figure 9.3:
A. Synaptic coupling function with zero mean as in
Eq. (9.16) with
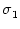 = 1 and
= 1 and
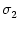 = 10. B. Fourier transform of the coupling function shown in A; cf. Eq. (9.18). C. Gain function
g(u) = {1 + exp[
= 10. B. Fourier transform of the coupling function shown in A; cf. Eq. (9.18). C. Gain function
g(u) = {1 + exp[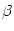 (x -
(x - 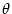 )]}-1 with
)]}-1 with 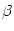 = 5 and
= 5 and
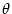 = 1. The dashing indicates that part of the graph where the
slope exceeds the critical slope s * . D. Derivative of
the gain function shown in C (solid line) and critical slope
s * (dashed line).
= 1. The dashing indicates that part of the graph where the
slope exceeds the critical slope s * . D. Derivative of
the gain function shown in C (solid line) and critical slope
s * (dashed line).
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...h}
{\bf D}
\par\includegraphics[width=\textwidth]{df_1_5.ps.gz}
\end{minipage}](img1427.gif) |
As a first step we search for a homogeneous solution. If we substitute
u(x, t) = u(t) in Eq. (9.4) we find
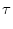 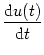 = - u(t) + Iext . = - u(t) + Iext . |
(9.16) |
The term containing the integral drops out because of
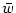 = 0. This
differential equation has a single stable fixed point at
u0 = Iext.
This situation corresponds to the graphical solution of Fig. 9.2 with the dashed lines replaced by vertical lines (`infinite slope').
= 0. This
differential equation has a single stable fixed point at
u0 = Iext.
This situation corresponds to the graphical solution of Fig. 9.2 with the dashed lines replaced by vertical lines (`infinite slope').
We still have to check the stability of the homogenous solution
u(x, t) = u0
with respect to inhomogeneous perturbations. In the present case, the Fourier
transform of w,
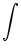 dx w(x) ei k x = dx w(x) ei k x = 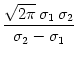 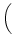 e-k2 e-k2 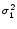 /2 - e-k2 /2 - e-k2 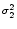 /2 /2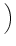 , , |
(9.17) |
vanishes at k = 0 and has its maxima at
At the maximum, the amplitude of the Fourier transform has a value of
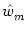 = = 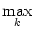 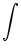 dx w(x) ei k x = dx w(x) ei k x = 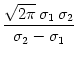  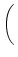 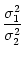 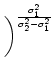 - - 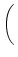 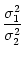 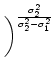 ![$\displaystyle \left.\vphantom{ \left( \frac{\sigma_1^2}{\sigma_2^2} \right )^{\...
...a_1^2}{\sigma_2^2} \right )^{\frac{\sigma_2^2}{\sigma_2^2-\sigma_1^2}} }\right]$](img1444.gif) , , |
(9.19) |
cf. Fig. 9.3B.
We use this result in Eqs. (9.12)
and (9.13) and conclude that
stable homogeneous solutions can
only be found for those parts of the graph of the output
function f (u) where the slope s = g'(u) does not exceed the critical
value
s * = 1/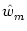 ,
,
Figure Fig. 9.3 shows that depending on the choice of
coupling w and gain functions g a certain interval for the external
input exists without a corresponding stable homogeneous solution. In this
parameter domain a phenomenon called pattern formation can be observed: Small
fluctuations around the homogeneous state grow exponentially until a
characteristic pattern of regions with low and high activity has developed;
cf. Fig. 9.4.
Figure 9.4:
Spontaneous pattern formation in a one-dimensional sheet
of neurons with `mexican-hat' type of interaction and homogeneous
external stimulation. The parameters for the coupling function and
the output function are the same as in Fig. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) . The graphs show the evolution in time of the spatial
distribution of the average membrane potential u(x, t). A. For
Iext = 0.4 the homogeneous low-activity state is
stable, but it looses stability at
Iext = 0.6 (B). Here, small initial fluctuations in the membrane potential
grow exponentially and result in a global pattern of regions with
high and low activity. C. Similar situation as in B, but
with
Iext = 1.4. D. Finally, at
Iext = 1.6 the homogeneous high-activity mode is stable.
. The graphs show the evolution in time of the spatial
distribution of the average membrane potential u(x, t). A. For
Iext = 0.4 the homogeneous low-activity state is
stable, but it looses stability at
Iext = 0.6 (B). Here, small initial fluctuations in the membrane potential
grow exponentially and result in a global pattern of regions with
high and low activity. C. Similar situation as in B, but
with
Iext = 1.4. D. Finally, at
Iext = 1.6 the homogeneous high-activity mode is stable.
![\begin{minipage}{0.48\textwidth}
{\bf A} ($I^{\text{ext}}=0.4$)
\par\includegra...
...t}}=1.6$)
\par\includegraphics[width=\textwidth]{blobs_16.ps.gz}
\end{minipage}](img1448.gif) |
9.1.3 `Blobs' of activity: inhomogeneous states
From a computational point of view bistable systems are of particular interest
because they can be used as `memory units'. For example a homogeneous
population of neurons with all-to-all connections can exhibit a bistable
behavior where either all neurons are quiescent or all neurons are firing
at their maximum rate. By switching between the inactive and the active
state, the neuronal population would be able to represent, store, or retrieve
one bit of information. The exciting question that arises now is whether a
neuronal net with distance-dependent coupling w(| x - y|) can store more
than just a single bit of information, but spatial patterns of
activity. Sensory input, e.g., visual stimulation, could switch part of the
network to its excited state whereas the unstimulated part would remain in its
resting state. Due to bistability this pattern of activity could be preserved
even if the stimulation is turned off again and thus provide a neuronal
correlate of working memory.
Let us suppose we prepare the network in a state where neurons in one spatial
domain are active and all remaining neurons are quiescent. Will the network
stay in that configuration? In other words, we are looking for an
`interesting' stationary solution u(x) of the field equation (9.4). The borderline where quiescent and active domains of the network
meet is obviously most critical to the function of the network as a memory
device. To start with the simplest case with a single borderline, we
consider a one-dimensional spatial pattern where the activity changes at x = 0
from the low-activity to the high-activity state. This pattern could be the
result of inhomogeneous stimulation in the past, but since we are interested
in a memory state we now assume that the external input is simply constant,
i.e.,
Iext(x, t) = Iext. Substitution of the ansatz
u(x, t) = u(x) into the field equation yields
u(x) - Iext = 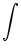 dy w(| x - y|) g[u(y)] . dy w(| x - y|) g[u(y)] . |
(9.21) |
This is a nonlinear integral equation for the unknown function
u(x).
We can find a particular solution of Eq. (9.22) if we replace the
output function by a simple step function, e.g.,
g(u) = 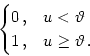 |
(9.22) |
In this case g[u(x)] is either zero or one and we can exploit
translation invariance to define g[u(x)] = 1 for x > 0 and g[u(x)] = 0
for x < 0 without loss of generality. The right-hand side of Eq. (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.gif) ) does now no longer depend on u and we find
) does now no longer depend on u and we find
u(x) = Iext + 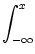 dz w(| z|) , dz w(| z|) , |
(9.23) |
and in particular
u(0) = Iext + 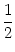 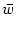 . . |
(9.24) |
with
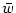 =
= 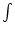 dy w(| y|). We have calculated this
solution under the assumption that g[u(x)] = 1 for x > 0 and g[u(x)] = 0
for x < 0. This assumption imposes a self-consistency condition on the
solution, namely that the membrane potential reaches the threshold
dy w(| y|). We have calculated this
solution under the assumption that g[u(x)] = 1 for x > 0 and g[u(x)] = 0
for x < 0. This assumption imposes a self-consistency condition on the
solution, namely that the membrane potential reaches the threshold 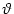 at x = 0. A solution in form of a stationary border between quiescent and
active neurons can therefore only be found, if
at x = 0. A solution in form of a stationary border between quiescent and
active neurons can therefore only be found, if
If the external stimulation is either smaller or greater than this
critical value, then the border will propagate to the right or to the
left.
Following the same line of reasoning, we can also look for a localized `blob'
of activity. Assuming that g[u(x)] = 1 for
x 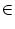 [x1, x2] and g[u(x)] = 0
outside this interval leads to a self-consistency condition of the form
[x1, x2] and g[u(x)] = 0
outside this interval leads to a self-consistency condition of the form
Iext = 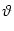 - - 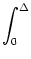 dx w(x) , dx w(x) , |
(9.26) |
with
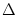 = x2 - x1. The mathematical arguments are qualitatively the same,
if we replace the step function by a more realistic smooth gain function.
= x2 - x1. The mathematical arguments are qualitatively the same,
if we replace the step function by a more realistic smooth gain function.
Figure 9.5 shows that solutions in the form of sharply localized
excitations exist for a broad range of external stimulations. A simple
argument also shows that the width 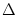 of the blob is stable if
w(
of the blob is stable if
w(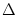 ) < 0 (Amari, 1977b). In this case blobs of activity can be
induced without the need of fine tuning the parameters in order to fulfill the
self-consistency condition, because the width of the blob will adjust itself
until stationarity is reached and Eq. (9.27) holds; cf. Fig. 9.5A.
) < 0 (Amari, 1977b). In this case blobs of activity can be
induced without the need of fine tuning the parameters in order to fulfill the
self-consistency condition, because the width of the blob will adjust itself
until stationarity is reached and Eq. (9.27) holds; cf. Fig. 9.5A.
Figure 9.5:
Localized `blobs' of activity. A. A small initial
perturbation develops into a stable blob of activity. B. Stationary
profile of a localized excitation for various amounts of external
stimulation (
Iext = 0, 0.5,..., 0.3 in order of increasing
width). Note that for strong stimuli neurons in the center of the
activity blob are less active than those close to the edge of the blob.
![\begin{minipage}[t]{0.48\textwidth}
{\bf A}
\par\includegraphics[width=\textwid...
...ar\vspace{5mm}
\includegraphics[width=\textwidth]{blob_b.ps.gz}
\end{minipage}](img1451.gif) |
9.1.3.1 Example: An application to orientation selectivity in V1
Stable localized blobs of activity may not only be related to memory states
but also to the processing of sensory information. A nice example is the model
of Ben-Yishai et al. (1995) [see also Hansel and Sompolinsky (1998)] that aims at a description
of orientation selectivity in the visual cortex.
It is found experimentally that cells from the primary visual cortex (V1)
respond preferentially to lines or bars that have a certain orientation within
the visual field. There are neurons that `prefer' vertical bars, others
respond maximally to bars with a different orientation (Hubel, 1995). Up to
now it is still a matter of debate where this orientation selectivity does
come from. It may be the result of the wiring of the input to the visual
cortex, i.e., the wiring of the projections from the LGN to V1, or it may
result from intra-cortical connections, i.e., from the wiring of the neurons
within V1, or both. Here we will investigate the extent to which
intra-cortical projections can contribute to
orientation selectivity.
We consider a network of neurons forming a so-called hypercolumn.
These are
neurons with receptive fields which correspond to roughly the same zone in the
visual field but with different preferred orientations. The orientation of a
bar at a given position within the visual field can thus be coded faithfully
by the population activity of the neurons from the corresponding hypercolumn.
Instead of using spatial coordinates to identify a neuron in the cortex, we
label the neurons in this section by their preferred orientation 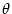 which may vary from -
which may vary from - 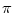 /2 to +
/2 to + 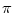 /2. In doing so we assume that the
preferred orientation is indeed a good ``name tag'' for each neuron so that
the synaptic coupling strength can be given in terms of the preferred
orientations of pre- and postsynaptic neuron. Following the formalism
developed in the previous sections, we assume that the synaptic coupling
strength w of neurons with preferred orientation
/2. In doing so we assume that the
preferred orientation is indeed a good ``name tag'' for each neuron so that
the synaptic coupling strength can be given in terms of the preferred
orientations of pre- and postsynaptic neuron. Following the formalism
developed in the previous sections, we assume that the synaptic coupling
strength w of neurons with preferred orientation 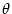 and
and 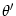 is a symmetric function of the difference
is a symmetric function of the difference
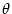 -
- 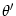 , i.e.,
w = w(|
, i.e.,
w = w(|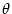 -
- 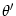 |). Since we are dealing with angles from
[-
|). Since we are dealing with angles from
[- 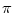 /2, +
/2, + 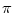 /2] it is natural to assume that all functions are
/2] it is natural to assume that all functions are
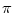 -periodic so that we can use Fourier series to characterize
them. Non-trivial results are obtained even if we retain only the first two
Fourier components of the coupling function,
-periodic so that we can use Fourier series to characterize
them. Non-trivial results are obtained even if we retain only the first two
Fourier components of the coupling function,
w(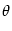 - - 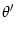 ) = w0 + w2 cos[2( ) = w0 + w2 cos[2(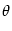 - - 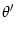 )] . )] . |
(9.27) |
Similarly to the intra-cortical projections we take the (stationary)
external input from the LGN as a function of the difference of the
preferred orientation 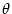 and the orientation of the stimulus
and the orientation of the stimulus
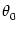 ,
,
Iext(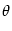 ) = c0 + c2 cos[2( ) = c0 + c2 cos[2(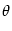 - - 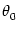 )] . )] . |
(9.28) |
Here, c0 is the mean of the input and c2 describes the
modulation of the input that arises from anisotropies in the
projections from the LGN to V1.
In analogy to Eq. (9.4) the field equation for the present
setup has thus the form
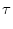 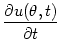 = - u( = - u(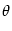 , t) + , t) + 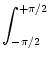 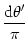 w(| w(|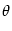 - - 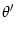 |) g[u( |) g[u(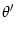 , t)] + Iext( , t)] + Iext(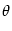 ) . ) . |
(9.29) |
We are interested in the distribution of the neuronal activity within
the hypercolumn as it arises from a stationary external stimulus with
orientation 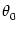 . This will allow us to study the role of
intra-cortical projections in sharpening orientation selectivity.
. This will allow us to study the role of
intra-cortical projections in sharpening orientation selectivity.
In order to obtain conclusive results we have to specify the form
of the gain function g. A particularly simple case is the
step-linear function,
g(u) = [u]+ 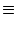 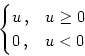 . . |
(9.30) |
The idea behind this ansatz is that neuronal firing usually increases
monotonously once the input exceeds a certain threshold. Within
certain boundaries this increase in the firing rate is approximatively
linear. If we assume that the average membrane potential u stays
within these boundaries and that, in addition,
u(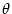 , t) is always
above threshold, then we can replace the gain function g in
Eq. (9.30) by the identity function. We are thus left
with the following linear equation for the stationary
distribution of the average membrane potential,
, t) is always
above threshold, then we can replace the gain function g in
Eq. (9.30) by the identity function. We are thus left
with the following linear equation for the stationary
distribution of the average membrane potential,
u(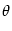 ) = ) = 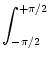 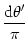 w(| w(|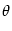 - - 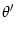 |) u( |) u(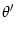 ) + Iext( ) + Iext(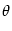 ) . ) . |
(9.31) |
This equation is solved by
u(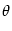 ) = u0 + u2 cos[2( ) = u0 + u2 cos[2(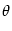 - - 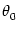 )] , )] , |
(9.32) |
with
u0 = 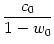 and u2 = and u2 = 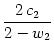 . . |
(9.33) |
As a result of the intra-cortical projections, the modulation u2 of
the response of the neurons from the hypercolumn is thus amplified by
a factor 2/(2 - w2) as compared to the modulation of the input
c2.
Figure 9.6:
Activity profiles (solid line) that result from stationary
external stimulation (dashed line) in a model of orientation
selectivity. A. Weak modulation (c0 = 0.8, c2 = 0.2) of the
external input results in a broad activity profile; cf. eqstat
theta. B. Strong modulation (c0 = 0.6, c2 = 0.4) produces a narrow
profile; cf. Eq. (9.35). Other parameters are
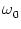 = 0,
= 0,
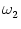 = 1,
= 1,
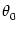 = 0.
= 0.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...h}
{\bf B}
\par\includegraphics[width=\textwidth]{profile_2.ps}
\end{minipage}](img1463.gif) |
In deriving Eq. (9.32) we have assumed that u stays
always above threshold so that we have an additional condition,
viz.,
u0 - | u2| > 0, in order to obtain a self-consistent solution.
This condition may be violated depending on the stimulus. In that case the
above solution is no longer valid and we have to take the nonlinearity of the
gain function into account, i.e., we have to replace Eq. (9.32) by
u(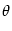 ) = ) = 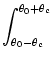 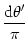 w(| w(|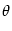 - - 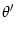 |) u( |) u(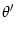 ) + Iext( ) + Iext(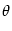 ) . ) . |
(9.34) |
Here,
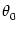 ±
±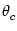 are the cutoff angles that define the interval
where u(
are the cutoff angles that define the interval
where u(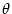 ) is positive. If we use the ansatz (9.33) in
the above equation, we obtain together with
u(
) is positive. If we use the ansatz (9.33) in
the above equation, we obtain together with
u(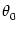 ±
±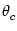 ) = 0 a set
of equations that can be solved for u0, u2, and
) = 0 a set
of equations that can be solved for u0, u2, and 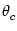 . Figure
9.6 shows two examples of the resulting activity profiles
g[u(
. Figure
9.6 shows two examples of the resulting activity profiles
g[u(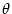 )] for different modulation depths of the input.
)] for different modulation depths of the input.
Throughout this section we have described neuronal populations in terms of an
averaged membrane potential and the corresponding firing rate. At least for
stationary input and a high level of noise this is indeed a good approximation
of the dynamics of spiking neurons. Figure 9.7 shows two
examples of a simulation based on SRM0 neurons with escape noise and a
network architecture that is equivalent to what we have used above. The
stationary activity profiles shown in Fig. 9.7 are
qualitatively identical to those of Fig. 9.6, small deviations in
the shape are due to a slightly different model [see Spiridon and Gerstner (2001) for
more details]. For low levels of noise, however, the description in terms of a
firing rate is no longer valid, because the state of asynchronous firing
becomes unstable (cf. Section 8.1) and neurons tend to
synchronize. The arising temporal structure in the firing times leads to a
destabilization of the stationary spatial structure (Laing and Chow, 2001). In the
low-noise limit localized ``blobs'' of activity are replaced by traveling
waves of spike activity, as we will see in Section 9.3.
Figure 9.7:
Activity profiles in a model of orientation selectivity obtained
by simulations based on SRM0 neurons (dots) compared to
the theoretical prediction (solid line).
A. No modulation of the recurrent
projections [
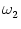 = 0; cf. Eq. (9.28)] leads only to a weak
modulation of the neuronal response. B. Excitatory coupling between
iso-oriented cells (
= 0; cf. Eq. (9.28)] leads only to a weak
modulation of the neuronal response. B. Excitatory coupling between
iso-oriented cells (
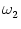 = 10) produces a sharp profile. [Taken from
Spiridon and Gerstner (2001)].
= 10) produces a sharp profile. [Taken from
Spiridon and Gerstner (2001)].
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\centerline{
\includegraphics[wid...
...terline{
\includegraphics[width=0.8\textwidth]{mona_b-edit.eps}} \end{minipage}](img1466.gif) |





Next: 9.2 Dynamic patterns of
Up: 9. Spatially Structured Networks
Previous: 9. Spatially Structured Networks
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...\bf B}
\par\includegraphics[width=\textwidth]{mexican_hat.ps.gz}
\end{minipage}](img1399.gif)
![]() u(t). We expect that a homogenous solution exists if
the external input is homogeneous as well, i.e., if
Iext(x, t)
u(t). We expect that a homogenous solution exists if
the external input is homogeneous as well, i.e., if
Iext(x, t) ![]() Iext(t).
Iext(t).
![]() u(t) into Eq. (9.4)
yields
u(t) into Eq. (9.4)
yields
![]() Iext. The fixed
points of Eq. (9.5) are solutions of
Iext. The fixed
points of Eq. (9.5) are solutions of
![\centerline{\includegraphics[width=0.45\textwidth]{fixed_points.ps.gz}}](img1410.gif)
![]() u0 is a homogeneous solution of Eq. (9.4),
i.e.,
u0 is a homogeneous solution of Eq. (9.4),
i.e.,
![\begin{multline}
\tau \, \frac{\partial}{\partial t} \delta u(x,t) =
-u_0 - \...
...a u(y,t)]
+ I^{\text{ext}}(x,t)
+{\mathcal{O}}(\delta u^2)
\,.
\end{multline}](img1414.gif)
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...h}
{\bf D}
\par\includegraphics[width=\textwidth]{df_1_5.ps.gz}
\end{minipage}](img1427.gif)
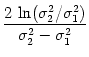
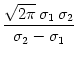
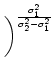 -
- 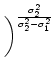
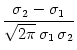
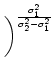 -
- 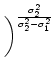
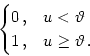
![]() [x1, x2] and g[u(x)] = 0
outside this interval leads to a self-consistency condition of the form
[x1, x2] and g[u(x)] = 0
outside this interval leads to a self-consistency condition of the form
![]() of the blob is stable if
w(
of the blob is stable if
w(![]() ) < 0 (Amari, 1977b). In this case blobs of activity can be
induced without the need of fine tuning the parameters in order to fulfill the
self-consistency condition, because the width of the blob will adjust itself
until stationarity is reached and Eq. (9.27) holds; cf. Fig. 9.5A.
) < 0 (Amari, 1977b). In this case blobs of activity can be
induced without the need of fine tuning the parameters in order to fulfill the
self-consistency condition, because the width of the blob will adjust itself
until stationarity is reached and Eq. (9.27) holds; cf. Fig. 9.5A.
![\begin{minipage}[t]{0.48\textwidth}
{\bf A}
\par\includegraphics[width=\textwid...
...ar\vspace{5mm}
\includegraphics[width=\textwidth]{blob_b.ps.gz}
\end{minipage}](img1451.gif)
![]() which may vary from -
which may vary from - ![]() /2 to +
/2 to + ![]() /2. In doing so we assume that the
preferred orientation is indeed a good ``name tag'' for each neuron so that
the synaptic coupling strength can be given in terms of the preferred
orientations of pre- and postsynaptic neuron. Following the formalism
developed in the previous sections, we assume that the synaptic coupling
strength w of neurons with preferred orientation
/2. In doing so we assume that the
preferred orientation is indeed a good ``name tag'' for each neuron so that
the synaptic coupling strength can be given in terms of the preferred
orientations of pre- and postsynaptic neuron. Following the formalism
developed in the previous sections, we assume that the synaptic coupling
strength w of neurons with preferred orientation ![]() and
and ![]() is a symmetric function of the difference
is a symmetric function of the difference
![]() -
- ![]() , i.e.,
w = w(|
, i.e.,
w = w(|![]() -
- ![]() |). Since we are dealing with angles from
[-
|). Since we are dealing with angles from
[- ![]() /2, +
/2, + ![]() /2] it is natural to assume that all functions are
/2] it is natural to assume that all functions are
![]() -periodic so that we can use Fourier series to characterize
them. Non-trivial results are obtained even if we retain only the first two
Fourier components of the coupling function,
-periodic so that we can use Fourier series to characterize
them. Non-trivial results are obtained even if we retain only the first two
Fourier components of the coupling function,
![]() and the orientation of the stimulus
and the orientation of the stimulus
![]() ,
,
![]() . This will allow us to study the role of
intra-cortical projections in sharpening orientation selectivity.
. This will allow us to study the role of
intra-cortical projections in sharpening orientation selectivity.
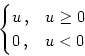 .
.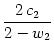 .
.![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...h}
{\bf B}
\par\includegraphics[width=\textwidth]{profile_2.ps}
\end{minipage}](img1463.gif)
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\centerline{
\includegraphics[wid...
...terline{
\includegraphics[width=0.8\textwidth]{mona_b-edit.eps}} \end{minipage}](img1466.gif)