We have seen that the intricate interplay of excitation and inhibition in locally coupled neuronal nets can result in the formation of complex patterns of activity. Neurons have been described by a graded-response type formalism where the `firing rate' is given as a function of the `average membrane potential'. This approach is clearly justified for a qualitative treatment of slowly varying neuronal activity. In the context of spatio-temporal patterns of neuronal activity, however, a slightly closer look is in order.
In the following we will dismiss the firing rate paradigm and use the
Spike Response Model instead in order to describe neuronal activity in
terms of individual action potentials. We start with a large number of
SRM neurons arranged on a two-dimensional grid. The synaptic coupling
strength w of neurons located at ![]() and
and ![]() is,
as hitherto, a function of their distance, i.e.,
w = w(|
is,
as hitherto, a function of their distance, i.e.,
w = w(|![]() -
- ![]() |). The response of a neuron to the
firing of one of its presynaptic neurons is described by a response
function
|). The response of a neuron to the
firing of one of its presynaptic neurons is described by a response
function ![]() and, finally, the afterpotential is given by a
kernel named
and, finally, the afterpotential is given by a
kernel named ![]() , as customary. The membrane potential of a neuron
located at
, as customary. The membrane potential of a neuron
located at ![]() is thus
is thus
Spikes are triggered whenever the membrane potential reaches the firing
threshold ![]() . This can be expressed in compact form as
. This can be expressed in compact form as
S(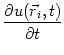 |
(9.45) |
Figure 9.11 shows the result of a computer simulation of a network consisting of 1000×1000 SRM neurons. The coupling function is mexican-hat shaped so that excitatory connections dominate on small and inhibitory connections on large distances. In a certain parameter regime the network exhibits an excitable behavior; cf. Section 9.2.2. Starting from a random initial configuration, a cloud of short stripes of neuronal activity evolves. These stripes propagate through the net and soon start to form rotating spirals with two, three or four arms. The spirals have slightly different rotation frequencies and in the end only a few large spirals with three arms will survive.
![\setlength{\fboxsep}{0cm} \centerline{
\begin{minipage}{50mm}
\centerline{\fbo...
...m=4 3 4 21, clip=true]
{fig03f.ps.gz}}}
\centerline{3000 ms}
\end{minipage} }](img1509.gif) |
Let us try to gain an analytic understanding of some of the phenomenon
observed in the computer simulations. To this end we suppose that the
coupling function w is slowly varying, i.e., that the distance
between two neighboring neurons is small as compared to the
characteristic length scale of w. In this case we can replace in
Eq. (9.45) the sum over all presynaptic neurons by an integral
over space. At the same time we drop the indices that label the
neurons on the grid and replace both h and S by continuous
functions of ![]() and t that interpolate in a suitable way between
the grid points for which they have been defined originally. This
leads to field equations
that describe the membrane potential
u(
and t that interpolate in a suitable way between
the grid points for which they have been defined originally. This
leads to field equations
that describe the membrane potential
u(![]() , t)
of neurons located at
, t)
of neurons located at ![]() ,
,
The approach sketched in Sections 9.3.1 and 9.3.2 (Kistler et al., 1998; Bressloff, 1999; Kistler, 2000) is presented for a network of a single population of neurons, but it can also be extended to coupled networks of excitatory and inhibitory neurons (Golomb and Ermentrout, 2001). In addition to the usual fast traveling waves that are found in purely excitatory networks, additional slow and non-continuous `lurching' waves appear in an appropriate parameter regime (Golomb and Ermentrout, 2001; Rinzel et al., 1998).
We start our analysis of the field equations (9.47) and (9.48) by looking for a particular solution in form of a plane front of excitation in a two-dimensional network. To this end we make an ansatz for the spike activity
| S(x, y, t) = |
(9.48) |
| u(x, y, t) = |
(9.49) |
| u(x = v t, y, t) = |
(9.50) |
![\begin{minipage}[t]{0.45\textwidth}
{\bf A}\\
\par\includegraphics[width=\text...
...\bf B}\\
\par\includegraphics[width=\textwidth]{disp_rel.ps.gz}
\end{minipage}](img1523.gif) |
The simulations show that the dynamics is dominated in large parts of the net by a regular pattern of stripes. These stripes are, apart from the centers of the spirals, formed by an arrangement of approximatively plane fronts. We can use the same ideas as above to look for such a type of solution. We make an ansatz,
S(x, y, t) = 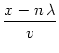 |
(9.51) |
| ufront(x, y, t) = |
(9.53) |
Using the fact that the membrane potential on each of the
wave fronts equals the firing threshold we find a relation between the
phase velocity and the wave length. This relation can be reformulated
as a dispersion relation for the wave number
k = 2![]() /
/![]() and the frequency
and the frequency
![]() = 2
= 2![]() v/
v/![]() . The dispersion relation,
which is shown in Fig. 9.12B for various values of the firing
threshold, fully characterizes the behavior of the wave.
. The dispersion relation,
which is shown in Fig. 9.12B for various values of the firing
threshold, fully characterizes the behavior of the wave.
A single front of excitation that travels through the net triggers a
single action potential in each neuron. In order to investigate the
stability of a traveling front of excitation we introduce the firing
time
t(![]() ) of a neuron located at
) of a neuron located at ![]() . The threshold
condition for the triggering of spikes can be read as an implicit
equation for the firing time as a function of space,
. The threshold
condition for the triggering of spikes can be read as an implicit
equation for the firing time as a function of space,
We are aiming at a linear stability analysis in terms of the firing
times (Bressloff, 1999). To this end we consider a
small perturbation
![]() t(x, y) which will be added to the solution of a
plane front of excitation traveling with velocity v in positive
x-direction, i.e.,
t(x, y) which will be added to the solution of a
plane front of excitation traveling with velocity v in positive
x-direction, i.e.,
| t(x, y) = x/v + |
(9.55) |
Figure 9.13 shows the result of a numerical
analysis of the stability equation (9.58). It turns out that
the lower branch of the v-![]() curve corresponds to unstable
solutions that are susceptible to two types of perturbation, viz.,
a perturbation with
Im(
curve corresponds to unstable
solutions that are susceptible to two types of perturbation, viz.,
a perturbation with
Im(![]() ) = 0 and a oscillatory perturbation
with
Im(
) = 0 and a oscillatory perturbation
with
Im(![]() )
)![]() 0. In addition, fronts with a velocity larger
than a certain critical velocity are unstable because of a form
instability with
Im(
0. In addition, fronts with a velocity larger
than a certain critical velocity are unstable because of a form
instability with
Im(![]() ) = 0 and
) = 0 and ![]() > 0. Depending on the
actual coupling function w, however, there may be a narrow
interval for the propagation velocity where plane fronts are stable;
cf. Fig. 9.13B.
> 0. Depending on the
actual coupling function w, however, there may be a narrow
interval for the propagation velocity where plane fronts are stable;
cf. Fig. 9.13B.
![\begin{minipage}[t]{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwid...
...\includegraphics[width=\textwidth]{v_vs_theta_2_stability.ps.gz}
\end{minipage}](img1532.gif) |
The stability of plane waves can be treated in a similar way as that of a plane front, we only have to account for the fact that each neuron is not firing only once but repetitively. We thus use the following ansatz for the firing times {tn(x, y)| n = 0,±1,±2,...} of a neuron located at (x,y),
tn(x, y) = 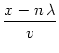 + + |
(9.57) |
For the sake of simplicity we neglect the contribution of the after
potential in Eq. (9.60), i.e., we assume that
![]() [n
[n ![]() /v] = 0 for n > 0. This assumption is justified for
short-lasting afterpotentials and a low firing frequency.
/v] = 0 for n > 0. This assumption is justified for
short-lasting afterpotentials and a low firing frequency.
As before, we concentrate on a particular form of the perturbations
![]() tn(x, y), namely
tn(x, y), namely
![]() tn(x, y) = exp[c (x - n
tn(x, y) = exp[c (x - n ![]() )] cos(
)] cos(![]() n) cos(
n) cos(![]() y). This corresponds to a sinusoidal
deformation of the fronts in y-direction described by
y). This corresponds to a sinusoidal
deformation of the fronts in y-direction described by ![]() together
with a modulation of their distance given by
together
with a modulation of their distance given by ![]() . If we substitute this
ansatz for the perturbation in Eq. (9.60) we obtain a set of equations
that can be reduced to two linearly independent equations for c,
. If we substitute this
ansatz for the perturbation in Eq. (9.60) we obtain a set of equations
that can be reduced to two linearly independent equations for c, ![]() ,
and
,
and ![]() . The complex roots of this system of equations determines the
stability of traveling waves, as it is summarized in Fig. 9.12.
. The complex roots of this system of equations determines the
stability of traveling waves, as it is summarized in Fig. 9.12.
![\begin{minipage}[t]{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwid...
... {\bf B}
\par\includegraphics[width=\textwidth]{disp_rel2.ps.gz}
\end{minipage}](img1542.gif) |
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.