




Next: 6.6 Limitations
Up: 6. Population Equations
Previous: 6.4 Asynchronous firing
Subsections
6.5 Interacting Populations and Continuum Models
In this section we extend the population equations
from a single homogeneous population
to several populations. We start in
Section 6.5.1
with interacting groups of neurons
and turn then in Section 6.5.2
to a continuum description.
6.5.1 Several Populations
Let us consider a network consisting of
several populations; cf. Fig. 6.14.
It is convenient to visualize the neurons as
being arranged in spatially separate pools, but this is not necessary.
All neurons could, for example, be physically localized in the same
column of the visual cortex. Within the column
we could define two pools,
one for excitatory and one for inhibitory neurons, for example.
Figure 6.14:
Several interacting populations of neurons.
![\hbox{\hspace{10mm}
\includegraphics[width=60mm]{Figs-ch-pop/pop-1b.eps}}](img1137.gif) |
We assume that neurons are homogeneous within each pool.
The activity of neurons in pool n is
An(t) = 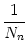 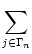 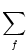 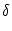 (t - tj(f)) (t - tj(f)) |
(6.113) |
where Nn is the number of neurons in pool n and 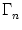 denotes the
set of neurons that belong to pool n. We assume that each neuron i in
pool n receives input from all neurons j in pool m with strength
wij = Jnm/Nm; cf. Fig. 6.15. The input potential to a neuron
i in group
denotes the
set of neurons that belong to pool n. We assume that each neuron i in
pool n receives input from all neurons j in pool m with strength
wij = Jnm/Nm; cf. Fig. 6.15. The input potential to a neuron
i in group 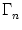 is generated by the spikes of all neurons in the network,
is generated by the spikes of all neurons in the network,
hi(t| ) ) |
= |
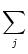 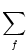 wij wij 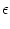 (t - (t -  , t - tj(f)) , t - tj(f)) |
|
| |
= |
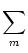 Jnm Jnm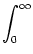 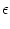 (t - (t -  , s) , s) 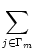 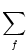 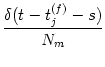 . . |
(6.114) |
We use Eq. (6.113) to replace the sum
on the right-hand side of Eq. (6.114) and obtain
hn(t| ) = ) = 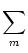 Jnm Jnm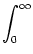 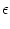 (t - (t -  , s) Am(t - s) ds . , s) Am(t - s) ds . |
(6.115) |
We have dropped the index i since
the input potential is the same for all neurons in pool n
that have fired their last spike at  .
Note that Eq. (6.115) is a straightforward
generalization of Eq. (6.8) and could have been
`guessed' immediately; external input
Iext
could be added
as in Eq. (6.8).
.
Note that Eq. (6.115) is a straightforward
generalization of Eq. (6.8) and could have been
`guessed' immediately; external input
Iext
could be added
as in Eq. (6.8).
In case of several populations, the dynamic equation (6.75) for the
population activity is to be applied to each pool activity separately, e.g.,
for pool n
An(t) = 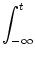 Pn(t | Pn(t | ) An( ) An( ) d ) d . . |
(6.116) |
Equation (6.116) looks simple and we may wonder
where the interactions between different pools come into play.
In fact, pool n is coupled to other populations via the potential hn
which determines the kernel
Pn(t |  ).
For example, with the escape noise model, we have
).
For example, with the escape noise model, we have
Pn(t| ) = f[un(t| ) = f[un(t| ) - ) - 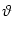 ] exp ] exp![$\displaystyle \left\{\vphantom{ \int_{\hat{t}}^t f[u_n(t'\vert\hat{t})-\vartheta] \, {\text{d}}t' \, }\right.$](img1144.gif) 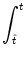 f[un(t'| f[un(t'| ) - ) - 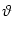 ] dt' ] dt' ![$\displaystyle \left.\vphantom{ \int_{\hat{t}}^t f[u_n(t'\vert\hat{t})-\vartheta] \, {\text{d}}t' \, }\right\}$](img1145.gif) |
(6.117) |
with
un(t| ) =
) = 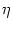 (t -
(t -  ) + hn(t|
) + hn(t| ),
with
hn(t|
),
with
hn(t| ) given by
(6.115).
Eqs. (6.115) - (6.117)
determine the dynamics of interacting pools
of Spike Response Model neurons with escape noise.
) given by
(6.115).
Eqs. (6.115) - (6.117)
determine the dynamics of interacting pools
of Spike Response Model neurons with escape noise.
Figure 6.15:
All neurons in group 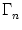 are coupled with
synaptic efficacy
wij = Jnn/Nn.
Each pair of neurons i, j with the presynaptic
j in groups Gammam and the postsynaptic neuron i in
are coupled with
synaptic efficacy
wij = Jnn/Nn.
Each pair of neurons i, j with the presynaptic
j in groups Gammam and the postsynaptic neuron i in 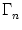 is
coupled via
wij = Jnm/Nm.
is
coupled via
wij = Jnm/Nm.
![\vbox{
% hbox\{a)\}
\hbox{\hspace{30mm}
\includegraphics[width=60mm]{Figs-ch-pop/severalpop.eps}}
}](img1146.gif) |
The fixed points of the activity in a network consisting of several
populations can be found as in Section 6.4. First we
determine for each pool the activity as a function of the total input Im
where gm is the gain function of neurons in pool m. Then we calculate
the total input current to neurons in pool m,
Im = 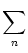 Jmn An . Jmn An . |
(6.119) |
Inserting Eq. (6.119) in (6.118) yields
the standard formula of artificial neural networks,
derived here for interacting populations of neurons.
6.5.2 Spatial Continuum Limit
The physical location of a neuron in a population
often reflects the task of a neuron.
In the auditory system, for example,
neurons are organized along an axis
that reflects the neurons' preferred
frequency. A neuron at one end of the axis
will respond maximally to low-frequency tones;
a neuron at the other end to high frequencies.
As we move along the axis the preferred
frequency changes gradually.
For neurons organized
along a one-dimensional axis or, more generally
in a spatially extended multidimensional network,
a description by discrete pools does not seem
appropriate. We will indicate in this section
that a transition from discrete pools to a continuous population
is possible. Here we give a short
heuristic motivation of the equations.
A thorough derivation along a slightly
different line of arguments will be performed in Chapter 9.
To keep the notation simple, we consider a
population of neurons that extends
along a one-dimensional axis; cf. Fig. 6.16.
We assume that the interaction
between a pair of neurons i, j depends only
on their location x or y on the line.
If the location of the presynaptic neuron is
y and that of the postsynaptic neuron is x,
then
wij = w(x, y).
In order to use Eq. (6.115),
we discretize space in segments of size d.
The number of neurons in the interval
[n d,(n + 1) d] is
Nn = 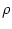 d
where
d
where 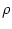 is the spatial density.
Neurons in that interval form the group
is the spatial density.
Neurons in that interval form the group 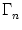 .
.
Figure 6.16:
In a spatially continuous ensemble of neurons,
the number of neurons in a segment d is N = 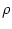 d.
The efficacy wij between two neurons depends
on their location.
The coupling strength between
a presynaptic neuron j at position
xj
d.
The efficacy wij between two neurons depends
on their location.
The coupling strength between
a presynaptic neuron j at position
xj 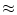 md and a postsynaptic
neuron i at location
xi
md and a postsynaptic
neuron i at location
xi 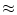 nd
is
wij
nd
is
wij 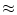 w(nd, md ).
w(nd, md ).
![\hbox{\hspace{10mm}
\includegraphics[width=60mm]{Figs-ch-pop/pop-contin.eps}}](img1150.gif) |
We change our notation with respect to
Eq.(6.115) and replace the subscript n
in hn and An by the spatial position
hn(t| ) ) |
 |
h(n d, t| ) = h(x, t| ) = h(x, t| ) ) |
(6.121) |
| An(t) |
 |
A(n d, t) = A(x, t) |
(6.122) |
Since the efficacy of a pair of neurons
with
i 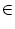
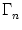 and
j
and
j 
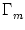 is by definition
wij = Jnm/Nm
with
Nm =
is by definition
wij = Jnm/Nm
with
Nm = 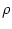 d,
we have
Jnm =
d,
we have
Jnm = 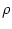 d w(n d, m d ).
We use this in Eq. (6.115) and find
d w(n d, m d ).
We use this in Eq. (6.115) and find
h(n d, t| ) = ) = 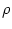 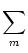 d w(n d, m d ) d w(n d, m d )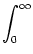 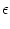 (t - (t -  , s) A(m d, t - s) ds . , s) A(m d, t - s) ds . |
(6.123) |
For d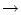 0, the summation on the right-hand side can
be replaced by an integral and we arrive at
0, the summation on the right-hand side can
be replaced by an integral and we arrive at
h(x, t| ) = ) = 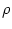 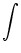 w(x, y) w(x, y)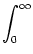 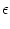 (t - (t -  , s) A(y, t - s) ds dy , , s) A(y, t - s) ds dy , |
(6.124) |
which is the final result.
The population activity has the dynamics
A(x, t) = 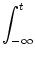 Px(t | Px(t | ) A(x, ) A(x, ) d ) d , , |
(6.125) |
where Px is the interval distribution for neurons
with input potential
h(x, t| ).
).
If we are interested in stationary states of asynchronous firing,
the activity
A(y, t) 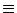 A0(y) can be calculated as before
with the help of the neuronal gain function g. The result is
in analogy to Eqs. (6.118) and (6.120)
A0(y) can be calculated as before
with the help of the neuronal gain function g. The result is
in analogy to Eqs. (6.118) and (6.120)
A0(x) = g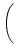 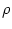 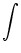 w(x, y) A0(y) dy w(x, y) A0(y) dy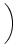 . . |
(6.126) |
In the case of SRM0 neurons, the input potential
h does not depend on the last firing time  so that Eq. (6.124) reduces to
so that Eq. (6.124) reduces to
h(x, t) = 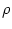 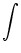 w(x, y) w(x, y)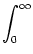 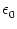 (s) A(y, t - s) ds dy . (s) A(y, t - s) ds dy . |
(6.127) |
We assume that the postsynaptic potential can
be approximated by an exponential function with
time constant 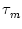 , i.e.,
, i.e.,
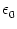 (s) =
(s) = 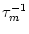 exp(- s/
exp(- s/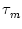 ).
Just as we did before in Eq. (6.87),
we can now transform Eq. (6.127) into
a differential equation,
).
Just as we did before in Eq. (6.87),
we can now transform Eq. (6.127) into
a differential equation,
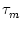 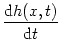 = - h(x, t) + = - h(x, t) + 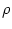 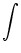 w(x, y) A(y, t) dy . w(x, y) A(y, t) dy . |
(6.128) |
If we make the additional assumption
that the activity A changes only slowly over time,
we may replace A by its stationary solution, i.e.,
A(y, t) = g[h(y, t)].
Here g[h(y, t)] is the single neuron firing rate
as a function of the total input potential.
For constant input current I0 and normalized input resistance
R = 1
we have h0 = I0.
In this case, we may identify g(h0) with the gain
function g(I0) of the neuron - and knowing this
we have chosen the same symbol g for both functions.
If we insert
A(y, t) = g[h(y, t)] in Eq. (6.128),
we arrive at an integro-differential equations for
the `field' h(x, t)
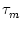 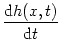 = - h(x, t) + = - h(x, t) + 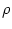 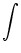 w(x, y) g[h(y, t)] dy . w(x, y) g[h(y, t)] dy . |
(6.129) |
We refer to Eq. (6.129) as
the neuronal
field equation (Amari, 1977a; Feldman and Cowan, 1975; Wilson and Cowan, 1973; Ellias and Grossberg, 1975).
It will be studied in detail
in Chapter 9.





Next: 6.6 Limitations
Up: 6. Population Equations
Previous: 6.4 Asynchronous firing
Gerstner and Kistler
Spiking Neuron Models. Single Neurons, Populations, Plasticity
Cambridge University Press, 2002
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.
![\hbox{\hspace{10mm}
\includegraphics[width=60mm]{Figs-ch-pop/pop-1b.eps}}](img1137.gif)
![\vbox{
% hbox\{a)\}
\hbox{\hspace{30mm}
\includegraphics[width=60mm]{Figs-ch-pop/severalpop.eps}}
}](img1146.gif)
![]() d
where
d
where ![]() is the spatial density.
Neurons in that interval form the group
is the spatial density.
Neurons in that interval form the group ![]() .
.
![\hbox{\hspace{10mm}
\includegraphics[width=60mm]{Figs-ch-pop/pop-contin.eps}}](img1150.gif)
![]() A0(y) can be calculated as before
with the help of the neuronal gain function g. The result is
in analogy to Eqs. (6.118) and (6.120)
A0(y) can be calculated as before
with the help of the neuronal gain function g. The result is
in analogy to Eqs. (6.118) and (6.120)
![]() so that Eq. (6.124) reduces to
so that Eq. (6.124) reduces to