In the subthreshold regime, the integrate-and-fire model with stochastic input (diffusive noise) can be mapped approximately onto an escape noise model with a certain escape rate f (Plesser and Gerstner, 2000). In this section, we motivate the mapping and the choice of f.
In the absence of a threshold, the membrane potential of an integrate-and-fire
model has a Gaussian probability distribution, around the noise-free reference
trajectory u0(t). If we take the threshold into account, the probability
density at
u = ![]() of the exact solution vanishes, since the threshold
acts as an absorbing boundary; see Eq. (5.92). Nevertheless, in
a phenomenological model, we can approximate the probability density near
u =
of the exact solution vanishes, since the threshold
acts as an absorbing boundary; see Eq. (5.92). Nevertheless, in
a phenomenological model, we can approximate the probability density near
u = ![]() by the `free' distribution
(i.e., without the threshold)
by the `free' distribution
(i.e., without the threshold)
We have seen in Eq. (5.97) that the variance
![]()
![]() u2(t)
u2(t)![]() of the free distribution rapidly approaches a constant value
of the free distribution rapidly approaches a constant value
![]() /2. We therefore replace the time dependent variance
2
/2. We therefore replace the time dependent variance
2![]()
![]() u(t)2
u(t)2![]() by its stationary value
by its stationary value ![]() . The right-hand side
of
Eq. (5.114) is then a function of the noise-free reference
trajectory only. In order to transform the left-hand side of
Eq. (5.114) into an escape rate, we divide both sides by
. The right-hand side
of
Eq. (5.114) is then a function of the noise-free reference
trajectory only. In order to transform the left-hand side of
Eq. (5.114) into an escape rate, we divide both sides by ![]() t. The firing intensity is thus
t. The firing intensity is thus
![\centerline{\includegraphics[width=60mm]{Fig-Gauss3a.eps}}](img919.gif) |
Let us now suppose that the neuron receives, at t = t0, an input current
pulse which causes a jump of the membrane trajectory by an amount
![]() u > 0; see Fig. (5.21). In this case the Gaussian distribution of
membrane potentials is shifted instantaneously across the threshold so
that there is a nonzero probability that the neuron fires exactly at t0.
To say it differently, the firing intensity
u > 0; see Fig. (5.21). In this case the Gaussian distribution of
membrane potentials is shifted instantaneously across the threshold so
that there is a nonzero probability that the neuron fires exactly at t0.
To say it differently, the firing intensity
![]() (t) = f[u0(t) -
(t) = f[u0(t) - ![]() ]
has a
]
has a ![]() peak at t = t0. The escape rate of Eq. (5.115),
however, cannot reproduce this
peak at t = t0. The escape rate of Eq. (5.115),
however, cannot reproduce this ![]() peak. More generally, whenever the
noise free reference trajectory increases with slope
peak. More generally, whenever the
noise free reference trajectory increases with slope
![]() > 0, we expect
an increase of the instantaneous rate proportional to
> 0, we expect
an increase of the instantaneous rate proportional to ![]() , because the
tail of the Gaussian distribution drifts across the threshold; cf.
Eq. (5.111). In order to take the drift into account, we
generalize Eq. (5.115) and study
, because the
tail of the Gaussian distribution drifts across the threshold; cf.
Eq. (5.111). In order to take the drift into account, we
generalize Eq. (5.115) and study
We emphasize that the right-hand side of Eq. (5.116) depends only on the dimensionless variable
x(t) = 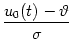 , , |
(5.117) |
To check the validity of the arguments that led to Eq. (5.116), let us compare the interval distribution generated by the diffusion model with that generated by the Arrhenius&Current escape model. We use the same input potential u0(t) as in Fig. 5.18. We find that the interval distributions PIdiff for the diffusive noise model and PIA&C for the Arrhenius&Current escape model are nearly identical; cf. Fig. (5.22). Thus the Arrhenius&Current escape model yields an excellent approximation to the diffusive noise model. We quantify the error of the approximation by the measure
Even though the Arrhenius&Current model has been designed for
sub-threshold stimuli, it also works remarkably well for super-threshold
stimuli with typical errors around E = 0.04. An obvious shortcoming of the
escape rate (5.116) is that the instantaneous rate decreases with u for
u > ![]() . The superthreshold behavior can be corrected if we replace the
Gaussian
exp(- x2) by
2 exp(- x2)/[1 + erf(- x)] (Herrmann and Gerstner, 2001a).
The subthreshold behavior remains unchanged compared to Eq. (5.116) but
the superthreshold behavior of the escape rate f becomes linear. With this
new escape rate the typical error E in the super-threshold regime is as small
as that in the subthreshold regime.
. The superthreshold behavior can be corrected if we replace the
Gaussian
exp(- x2) by
2 exp(- x2)/[1 + erf(- x)] (Herrmann and Gerstner, 2001a).
The subthreshold behavior remains unchanged compared to Eq. (5.116) but
the superthreshold behavior of the escape rate f becomes linear. With this
new escape rate the typical error E in the super-threshold regime is as small
as that in the subthreshold regime.
![\centerline{\includegraphics[width=80mm]{Plesser2a-edit.eps}}](img929.gif) |
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.