- 11.1.3.1 Example: Subtractive Normalization of
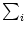 wi
wi
- 11.1.3.2 Example: Multiplicative Normalization of
|
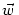 |
|
We would like to understand how activity-dependent learning rules influence the formation of connections between neurons in the brain. We will see that plasticity is controlled by the statistical properties of the presynaptic input that is impinging on the postsynaptic neuron. Before we delve into the analysis of the elementary Hebb rule we therefore need to recapitulate a few results from statistics and linear algebra.
A principal component analysis (PCA) is a standard technique to describe statistical properties of a set of high-dimensional data points and is usually performed in order to find those components of the data that show the highest variability within the set. If we think of the input data set as of a cloud of points in a high-dimensional vector space centered around the origin, then the first principal component is the direction of the longest axis of the ellipsoid that encompasses the cloud; cf. Fig. 11.1. If the data points consisted of, say, two separate clouds then the first principal component would give the direction of a line that connects the center points of the two clouds. A PCA can thus be used to break a large data set into separate clusters. In the following, we will quickly explain the basic idea and show that the first principal component gives the direction where the variance of the data is maximal.
![\centerline{\includegraphics[width=6cm]{Figs-ch-hebb-anal/ellipsoid.ps}}](img1710.gif) |
Let us consider an ensemble of data points
{![]() ,...,
,...,![]() }
drawn from a (high-dimensional) vector space, for example
}
drawn from a (high-dimensional) vector space, for example
![]()
![]()
![]() N. For this set of data points we define the correlation
matrix Cij as
N. For this set of data points we define the correlation
matrix Cij as
The principal components of the set
{![]() ,...,
,...,![]() } are defined as the eigenvectors of the
covariance matrix V. Note that V is symmetric, i.e.,
Vij = Vji. The
eigenvalues of V are thus real-valued and different eigenvectors are
orthogonal (Horn and Johnson, 1985). Furthermore, V is positive semi-definite since
} are defined as the eigenvectors of the
covariance matrix V. Note that V is symmetric, i.e.,
Vij = Vji. The
eigenvalues of V are thus real-valued and different eigenvectors are
orthogonal (Horn and Johnson, 1985). Furthermore, V is positive semi-definite since
| (11.3) |
We can sort the eigenvectors ![]() according to the size of the
corresponding eigenvalues
according to the size of the
corresponding eigenvalues
![]()
![]()
![]()
![]() ...
...![]() 0. The
eigenvector with the largest eigenvalue is called the first principal
component. It points in the direction where
the variance of the data is maximal. To see this we calculate the variance of
the projection of
0. The
eigenvector with the largest eigenvalue is called the first principal
component. It points in the direction where
the variance of the data is maximal. To see this we calculate the variance of
the projection of
![]() onto an arbitrary direction
onto an arbitrary direction ![]() that we
write as
that we
write as
![]() =
= ![]() ai
ai ![]() with
with
![]() ai2 = 1 so that
|
ai2 = 1 so that
|![]() | = 1. The variance
| = 1. The variance
![]() along
along ![]() is
is
| (11.4) |
In the following we analyze the evolution of synaptic weights using the
Hebbian learning rules that have been described in Chapter 10.
To do so, we consider a highly simplified scenario consisting of an analog
neuron that receives input from N presynaptic neurons with firing rates
![]() via synapses with weights wi; cf.
Fig. 11.2A. We think of the presynaptic neurons as `input
neurons', which, however, do not have to be sensory neurons. The input layer
could, for example, consist of neurons in the lateral geniculate nucleus (LGN)
that project to neurons in the visual cortex. We will see that the
statistical properties of the input control the evolution of synaptic weights.
via synapses with weights wi; cf.
Fig. 11.2A. We think of the presynaptic neurons as `input
neurons', which, however, do not have to be sensory neurons. The input layer
could, for example, consist of neurons in the lateral geniculate nucleus (LGN)
that project to neurons in the visual cortex. We will see that the
statistical properties of the input control the evolution of synaptic weights.
For the sake of simplicity, we model the presynaptic input as a set of static
patterns. Let us suppose that we have a total of p patterns
{![]() ;1 <
;1 < ![]() < p}. At each time step one of the patterns
< p}. At each time step one of the patterns
![]() is selected
at random and presented to the network by fixing the presynaptic rates at
is selected
at random and presented to the network by fixing the presynaptic rates at
![]() =
= ![]() . We call this the static-pattern
scenario.
The presynaptic activity drives
the postsynaptic neuron and the joint activity of pre- and postsynaptic
neurons triggers changes of the synaptic weights. The synaptic weights are
modified according to a Hebbian learning rule, i.e., according to the
correlation of pre- and postsynaptic activity; cf. Eq. (10.3).
Before the next input pattern is chosen, the weights are changed by an amount
. We call this the static-pattern
scenario.
The presynaptic activity drives
the postsynaptic neuron and the joint activity of pre- and postsynaptic
neurons triggers changes of the synaptic weights. The synaptic weights are
modified according to a Hebbian learning rule, i.e., according to the
correlation of pre- and postsynaptic activity; cf. Eq. (10.3).
Before the next input pattern is chosen, the weights are changed by an amount
![\hbox{{\bf A} \hspace{55mm} {\bf B}}
\hbox{\hspace{5mm}
\includegraphics[width...
...pace{10mm}
\includegraphics[width=65mm]{Figs-ch-hebb-anal/Fig-linear-b.eps}
}](img1757.gif) |
In a general rate model, the firing rate
![]() of the
postsynaptic neuron is given by a nonlinear function of the total input
of the
postsynaptic neuron is given by a nonlinear function of the total input
If we combine the learning rule (11.5)
with the linear rate model of Eq. (11.7)
we find after the presentation of pattern
![]()
We are interested in the long-term behavior of the synaptic weights.
To this end we assume that the
weight vector evolves along a more or less deterministic trajectory with only
small stochastic deviations that result from the randomness at which new input
patterns are chosen. This is, for example, the case if the learning rate is
small so that a large number of patterns has to be presented in order to
induce a substantial weight change. In such a situation it is sensible to
consider the expectation value of the weight vector, i.e., the weight vector
![]()
![]() (n)
(n)![]() averaged over the sequence
(
averaged over the sequence
(![]() ,
,![]() ,...,
,...,![]() ) of all patterns that so far have
been presented to the network. From Eq. (11.9) we find
) of all patterns that so far have
been presented to the network. From Eq. (11.9) we find
| (11.12) |
If we express the weight vector in terms of the eigenvectors ![]() of C,
of C,
| (11.13) |
| (11.14) |
From a data-processing point of view, the extraction of the first principle component of the input data set by a biologically inspired learning rule seems to be very compelling. There are, however, a few drawbacks and pitfalls. First, the above statement about the Hebbian learning rule is limited to the expectation value of the weight vector. We will see below that, if the learning rate is sufficiently low, then the actual weight vector is in fact very close to the expected one.
Second, while the direction of the weight vector moves in the direction of the principal component, the norm of the weight vector grows without bounds. We will see below in Section 11.1.3 that suitable variants of Hebbian learning allow us to control the length of the weight vector without changing its direction.
Third, principal components are only meaningful if the input data is normalized, i.e., distributed around the origin. This requirement is not consistent with a rate interpretation because rates are usually positive. This problem, however, can be overcome by learning rules such as the covariance rule of Eq. (10.10) that are based on the deviation of the rates from a certain mean firing rate. We will see in Section 11.2.4 that a spike-based learning rule can be devised that is sensitive only to deviations from the mean firing rate and can thus find the first principal component even if the input is not properly normalized.
![\hbox{{\bf A} \hspace{60mm} {\bf B}} \hbox{\hspace{5mm}
\includegraphics[width=...
...ace{20mm}
\includegraphics[width=50mm]{Figs-ch-hebb-anal/w-hebb-shifted.eps} }](img1805.gif) |
So far, we have derived the behavior of the expected weight vector,
![]()
![]()
![]() . Here we show that explicit averaging is not
necessary provided that learning is slow enough. In this case, the weight
vector is the sum of a large number of small changes. The weight dynamics is
thus `self-averaging' and the weight vector
. Here we show that explicit averaging is not
necessary provided that learning is slow enough. In this case, the weight
vector is the sum of a large number of small changes. The weight dynamics is
thus `self-averaging' and the weight vector ![]() can be well
approximated by its expectation value
can be well
approximated by its expectation value
![]()
![]()
![]() .
.
We start from the formulation of Hebbian plasticity in continuous time,
| (11.16) |
| (11.17) |
In the next time step a new pattern
![]() is presented so that the
weight is changed to
is presented so that the
weight is changed to
| wi(t + p |
(11.19) |
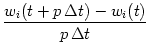 = ccorr2 = ccorr2 |
(11.20) |
| (11.21) |
We have seen in Section 11.1.2 that the simple learning rule (10.3) leads to exponentially growing weights. Since this is biologically not plausible, we must use a modified Hebbian learning rule that includes weight decrease and saturation; cf. Chapter 10.2. Particularly interesting are learning rules that lead to a normalized weight vector. Normalization is a desirable property since it leads to a competition between synaptic weights wij that converge on the same postsynaptic neuron i. Competition means that if a synaptic efficacy increases, it does so at the expense of other synapses that must decrease.
For a discussion of weight vector normalization two aspects are important,
namely what is normalized and how the normalization is
achieved. Learning rules can be designed to normalize either the sum
of weights,
![]() wij, or the quadratic norm,
|
wij, or the quadratic norm,
|![]() |2 =
|2 = ![]() wij2 (or any other norm on
wij2 (or any other norm on
![]() N). In the first case, the
weight vector is constrained to a plane perpendicular to the diagonal vector
N). In the first case, the
weight vector is constrained to a plane perpendicular to the diagonal vector
![]() = (1,..., 1); in the second case it is constrained to a
hyper-sphere; cf. Fig. 11.4.
= (1,..., 1); in the second case it is constrained to a
hyper-sphere; cf. Fig. 11.4.
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\centerline{
\includegraphics[wid...
...nterline{
\includegraphics[width=0.7\textwidth]{Fig-norm-a.eps}} \end{minipage}](img1811.gif) |
Second, the normalization of the weight vector can either be multiplicative or
subtractive. In the former case all weights are multiplied by a common factor
so that large weights wij are corrected by a larger amount than smaller
ones. In the latter case a common constant is subtracted from each weight.
Usually, subtractive normalization is combined with hard bounds
0![]() wij
wij![]() wmax in order to avoid runaway of individual weights.
Finally, learning rules may or may not fall into the class of local
learning rules that we have considered in Chapter 10.2.
wmax in order to avoid runaway of individual weights.
Finally, learning rules may or may not fall into the class of local
learning rules that we have considered in Chapter 10.2.
A systematic classification of various learning rules according to the above
three criteria has been proposed by Miller and MacKay (1994). Here we restrict
ourselves to two instances of learning with normalization properties which we
illustrate in the examples below. We start with the subtractive normalization
of the summed weights
![]() wij and turn then to a discussion of Oja's
rule as an instance of a multiplicative normalization of
wij and turn then to a discussion of Oja's
rule as an instance of a multiplicative normalization of
![]() wij2.
wij2.
In a subtractive normalization scheme the sum over all weights,
![]() wi, can be kept constant by subtracting the average total weight change,
N-1
wi, can be kept constant by subtracting the average total weight change,
N-1![]()
![]()
![]() , from each synapse after the weights have
been updated according to a Hebbian learning rule with
, from each synapse after the weights have
been updated according to a Hebbian learning rule with
![]()
![]() =
= ![]()
![]() wj
wj ![]()
![]() . Altogether, the
learning rule is of the form
. Altogether, the
learning rule is of the form
| = |
||
| = |
(11.22) |
In a similar way as in the previous section, we calculate the
expectation of the weight vector
![]()
![]() (n)
(n)![]() ,
averaged over the sequence of input patterns
(
,
averaged over the sequence of input patterns
(![]() ,
,![]() ,...),
,...),
| (11.23) |
![\hbox{{\bf A} \hspace{65mm} {\bf B}} \hbox{\hspace{5mm}
\includegraphics[width=...
... \hspace{20mm}
\includegraphics[width=50mm]{Figs-ch-hebb-anal/w-hebb-oja.eps}}](img1822.gif) |
Normalization of the sum of the weights,
![]() wi, needs an additional
criterion to prevent individual weights from perpetual growth. A more elegant
way is to require that the sum of the squared weights, i.e., the length of the
weight vector,
wi, needs an additional
criterion to prevent individual weights from perpetual growth. A more elegant
way is to require that the sum of the squared weights, i.e., the length of the
weight vector,
![]() wi2, remains constant. This restricts the evolution
of the weight vector to a sphere in the N dimensional weight space. In
addition, we can employ a multiplicative normalization scheme where all
weights all multiplied by a common factor instead of subtracting a common
constant. The advantage of multiplicative compared to subtractive
normalization is that small weights will not change their sign during the
normalization step.
wi2, remains constant. This restricts the evolution
of the weight vector to a sphere in the N dimensional weight space. In
addition, we can employ a multiplicative normalization scheme where all
weights all multiplied by a common factor instead of subtracting a common
constant. The advantage of multiplicative compared to subtractive
normalization is that small weights will not change their sign during the
normalization step.
In order to formalize the above idea we first calculate the `naïve'
weight change
![]() (n) in time step n according to the
common Hebbian learning rule,
(n) in time step n according to the
common Hebbian learning rule,
| (11.25) |
| (11.27) |
We may wonder whether Eq. (11.28) is a local learning rule. In
order to answer this question, we recall that the `naïve' weight change
![]()
![]() =
= ![]()
![]()
![]() uses only
pre- and postsynaptic information. Hence, we can rewrite Eq. (11.28) in
terms of the firing rates,
uses only
pre- and postsynaptic information. Hence, we can rewrite Eq. (11.28) in
terms of the firing rates,
In order to see that Oja's learning rule selects the
first principal component we show that the eigenvectors
{![]() ,...,
,...,![]() } of C are fixed points of the dynamics but that
only the eigenvector
} of C are fixed points of the dynamics but that
only the eigenvector ![]() with the largest eigenvalue is stable.
For any fixed weight vector
with the largest eigenvalue is stable.
For any fixed weight vector ![]() we can calculate the expectation
of the weight change in the next time step by averaging over the whole
ensemble of input patterns
{
we can calculate the expectation
of the weight change in the next time step by averaging over the whole
ensemble of input patterns
{![]() ,
,![]() ,...}.
With
,...}.
With
![]()
![]()
![]() (n)
(n)![]() =
= ![]() C
C ![]() we find from Eq. (11.28)
we find from Eq. (11.28)
| (11.31) |
Most neurons of the visual system respond only to stimulation from a narrow region within the visual field. This region is called the receptive field of that neuron. Depending on the precise position of a narrow bright spot within the receptive field the corresponding neuron can either show an increase or a decrease of the firing rate relative to its spontaneous activity at rest. The receptive field is subdivided accordingly into `ON' and `OFF' regions in order to further characterize neuronal response properties. Bright spots in an ON region increase the firing rate whereas bright spots in an OFF region inhibit the neuron.
Different neurons have different receptive fields, but as a general rule, neighboring neurons have receptive fields that `look' at about the same region of the visual field. This is what is usually called the retinotopic organization of the neuronal projections - neighboring points in the visual field are mapped to neighboring neurons of the visual system.
The visual system forms a complicated hierarchy of interconnected cortical areas where neurons show increasingly complex response properties from one layer to the next. Neurons from the lateral geniculate nucleus (LGN), which is the first neuronal relay of visual information after the retina, are characterized by so-called center-surround receptive fields. These are receptive fields that consist of two concentric parts, an ON region and an OFF region. LGN neurons come in two flavors, as ON-center and OFF-center cells. ON-center cells have a ON-region in the center of their receptive field that is surrounded by a circular OFF-region. In OFF-center cells the arrangement is the other way round; a central OFF-region is surrounded by an ON-region; cf. Fig. 11.6.
Neurons from the LGN project to the primary visual cortex (V1), which is the first cortical area involved in the processing of visual information. In this area neurons can be divided into `simple cells' and 'complex cells'. In contrast to LGN neurons, simple cells have asymmetric receptive fields which results in a selectivity with respect to the orientation of a visual stimulus. The optimal stimulus for a neuron with a receptive field such as that shown in Fig. 11.6D, for example, is a light bar tilted by about 45 degrees. Any other orientation would also stimulate the OFF region of the receptive field leading to a reduction of the neuronal response. Complex cells have even more intriguing properties and show responses that are, for example, selective for movements with a certain velocity and direction (Hubel, 1995).
![\begin{minipage}[t]{0.23\textwidth}
{\bf A}
\par\vspace{3mm}\hfill
\includegra...
...ncludegraphics[height=0.8\textwidth]{Figs-ch-hebb-anal/rf_d.eps}
\end{minipage}](img1846.gif) |
It is still a matter of debate how the response properties of simple cells arise. The original proposal by Hubel and Wiesel (1962) was that orientation selectivity is a consequence of the specific wiring between LGN and V1. Several center-surround cells with slightly shifted receptive fields should converge on a single V1 neuron so as to produce the asymmetric receptive field of simple cells. Alternatively (or additionally), the intra-cortical dynamics can generate orientation selectivity by enhancing small asymmetries in neuronal responses; cf. Section 9.1.3. In the following, we pursue the first possibility and try to understand how activity-dependent processes during development can lead to the required fine-tuning of the synaptic organization of projections from the LGN to the primary visual cortex (Miller, 1995,1994; Miller et al., 1989; Linsker, 1986c,b,a; Wimbauer et al., 1997a,b; MacKay and Miller, 1990).
We are studying a model that consists of a two-dimensional layer of cortical
neurons (V1 cells) and two layers of LGN neurons, namely one layer of
ON-center cells and one layer of OFF-center cells; cf. Fig. 11.7A.
In each layer, neurons are labeled by their position and projections between
the neurons are given as a function of their positions. Intra-cortical
projections, i.e., projections between cortical neurons, are denoted by
wV1, V1(![]() ,
,![]() ), where
), where ![]() and
and ![]() are
the position of the pre- and the postsynaptic neuron, respectively.
Projections from ON-center and OFF-center LGN neurons to the cortex are
denoted by
wV1, ON(
are
the position of the pre- and the postsynaptic neuron, respectively.
Projections from ON-center and OFF-center LGN neurons to the cortex are
denoted by
wV1, ON(![]() ,
,![]() ) and
wV1, OFF(
) and
wV1, OFF(![]() ,
,![]() ), respectively.
), respectively.
![\hbox{{\bf A} \hspace{75mm} {\bf B}} \hbox{\hspace{10mm}
\includegraphics[width...
...degraphics[width=35mm]{Figs-ch-hebb-anal/Fig-arborization.eps}
\vspace{4mm}} }](img1849.gif) |
In the following we are interested in the evolution of the weight distribution
of projections from the LGN to the primary visual cortex. We thus take
wV1, ON(![]() ,
,![]() ) and
wV1, OFF(
) and
wV1, OFF(![]() ,
,![]() )
as the dynamic variables of the model. Intra-cortical projections are supposed
be constant and dominated by short-range excitation, e.g.,
)
as the dynamic variables of the model. Intra-cortical projections are supposed
be constant and dominated by short-range excitation, e.g.,
wV1, V1(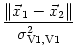 |
(11.32) |
As in the previous section we consider - for the sake of simplicity -
neurons with a linear gain function. The firing rate
![]() (
(![]() )
of a cortical neuron at position
)
of a cortical neuron at position ![]() is thus given by
is thus given by
Due to the intra-cortical interaction the cortical activity
![]() shows up on both sides of the equation. Since this is a linear equation it can
easily be solved for
shows up on both sides of the equation. Since this is a linear equation it can
easily be solved for
![]() . To do so we write
. To do so we write
![]() (
(![]() ) =
) = ![]()
![]()
![]() (
(![]() ), where
), where
![]() is the Kronecker
is the Kronecker
![]() that is one for
that is one for
![]() =
= ![]() and vanishes otherwise. Equation
(11.33) can thus be rewritten as
and vanishes otherwise. Equation
(11.33) can thus be rewritten as
| (11.33) |
| (11.35) |
We expect that the formation of synapses between LGN and V1 is driven by correlations in the input. In the present case, these correlations are due to the retinotopic organization of projections from the retina to the LGN. Neighboring LGN neurons receiving stimulation from similar regions of the visual field are thus correlated to a higher degree than neurons that are more separated. If we assume that the activity of individual photoreceptors on the retina is uncorrelated and that each LGN neuron integrates the input from many of these receptors then the correlation of two LGN neurons can be calculated from the form of their receptive fields. For center-surround cells the correlation is a Mexican hat-shaped function of their distance (Miller, 1994; Wimbauer et al., 1997a), e.g.,
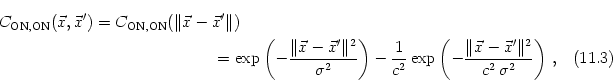
In the present formulation of the model each LGN cell can contact every neuron
in the primary visual cortex. In reality, each LGN cell sends one axon to the
cortex. Though this axon may split into several branches its synaptic contacts
are restricted to small region of the cortex; cf. Fig. 11.7B. We
take this limitation into account by defining an arborization function
A(![]() ,
,![]() ) that gives the a
priori probability that a connection between a LGN cell at location
) that gives the a
priori probability that a connection between a LGN cell at location ![]() and a cortical cell at
and a cortical cell at ![]() is formed (Miller et al., 1989). The
arborization is a rapidly decaying function of the distance, e.g.,
is formed (Miller et al., 1989). The
arborization is a rapidly decaying function of the distance, e.g.,
To describe the dynamics of the weight distribution we adopt a modified form of Hebb's learning rule that is completed by the arborization function,
| (11.37) |
If we use Eq. (11.34) and assume that learning is slow enough so that we can rely on the correlation functions to describe the evolution of the weights, we find
Expression (11.41) is still a linear equation for the weights
and nothing exciting can be expected. A prerequisite for pattern formation is
competition between the synaptic weights. Therefore, the above learning rule
is extended by a term
wV1, ON/OFF(![]() ,
,![]() )
) ![]() (
(![]() )2 that leads to weight vector normalization and
competition; cf. Oja's rule, Eq. (10.11).
)2 that leads to weight vector normalization and
competition; cf. Oja's rule, Eq. (10.11).
Many of the standard techniques for nonlinear systems that we have already encountered in the context of neuronal pattern formation in Chapter 9 can also be applied to the present model (Wimbauer et al., 1998; MacKay and Miller, 1990). Here, however, we will just summarize some results from a computer simulation consisting of an array of 8×8 cortical neurons and two times 20×20 LGN neurons. Figure 11.8 shows a typical outcome of such a simulation. Each of the small rectangles shows the receptive field of the corresponding cortical neuron. A bright color means that the neuron responds with an increased firing rate to a bright spot at that particular position within its receptive field; dark colors indicate inhibition.
There are two interesting aspects. First, the evolution of the synaptic weights has lead to asymmetric receptive fields, which give rise to orientation selectivity. Second, the structure of the receptive fields of neighboring cortical neurons are similar; neuronal response properties thus vary continuously across the cortex. The neurons are said to form a map for, e.g., orientation.
The first observation, the breaking of the symmetry of LGN receptive fields, is characteristic for all pattern formation phenomena. It results from the instability of the homogeneous initial state and the competition between individual synaptic weights. The second observation, the smooth variation of the receptive fields across the cortex, is a consequence of the excitatory intra-cortical couplings. During the development, neighboring cortical neurons tend to be either simultaneously active or quiescent and due to the activity dependent learning rule similar receptive fields are formed.
![\hbox{\hspace{20mm}
\includegraphics[width=80mm]{Figs-ch-hebb-anal/Stefan_new.eps} }](img1881.gif) |
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.