In the previous section we have seen that the evolution of synaptic weights under a rate-based learning rule depends on correlations in the input. What happens, if the rate-based learning rule is replaced by a spike-time dependent one?
In Section 11.2.1 we will derive an equation that
relates the expectation value of the weight vector to statistical properties
of pre- and postsynaptic spike trains. We will see that spike-time dependent
plasticity is sensitive to spatial and temporal correlations in the
input. In certain particularly simple cases spike-spike correlations can be
calculated explicitly. This is demonstrated in Section ![]() in the context of a linear Poisson neuron. This neuron model
is also used
in Section 11.2.3
for a comparison of spike-based and rate-based learning rules as
well as
in Section 11.2.4 where we revisit the static-pattern
scenario of Section 11.1.2. Finally,
in Section 11.2.5, we discuss the impact of
stochastic spike arrival on the synaptic weights and derive a Fokker-Planck
equation that describes the temporal evolution of the weight distribution.
in the context of a linear Poisson neuron. This neuron model
is also used
in Section 11.2.3
for a comparison of spike-based and rate-based learning rules as
well as
in Section 11.2.4 where we revisit the static-pattern
scenario of Section 11.1.2. Finally,
in Section 11.2.5, we discuss the impact of
stochastic spike arrival on the synaptic weights and derive a Fokker-Planck
equation that describes the temporal evolution of the weight distribution.
We will generalize the analysis of Hebbian learning that has been developed in Section 11.1 to spike-based learning rules based on the phenomenological model of Section 10.3.1. In this model the synaptic weight wij(t) is a piecewise continuous function of time with steps whenever a presynaptic spike arrives or when a postsynaptic action potential is triggered, i.e.,
In the previous section we have considered presynaptic firing rates ![]() as
random variables drawn from an ensemble of input patterns
as
random variables drawn from an ensemble of input patterns ![]() . The
output rate, however, was a deterministic function of the neuronal input. In
the context of spike-time dependent plasticity, we consider the set of
presynaptic spike arrival times
(tj1, tj2,...) as a random variable.
The underlying `randomness' may have several reasons. For example, different
stimulation paradigms may be selected one by one in very much the same way as
we have selected a new input pattern in the previous section. In contrast to
the rate model, we do not want to restrict ourselves to deterministic neuron
models. Hence, the randomness can also be produced by a stochastic neuron
model that is used in order account for noise; cf. Chapter 5. In this
case, the output spike train can be a random variable even if the input spike
trains are fixed. A simple example is the Poisson neuron model that generates
output spikes via an inhomogeneous Poisson process with an intensity that is a
function of the membrane potential. In any case, we consider the set of spike
trains
(S1,..., Si, Sj,..., SN), i.e., pre- and postsynaptic
trains, to be drawn from a stochastic ensemble. The specific properties of the
chosen neuron model are thus implicitly described by the association of pre-
and postsynaptic trains within the ensemble. Note that this formalism includes
deterministic models as a special case, if the ensemble contains only a single
postsynaptic spike train for any given set of presynaptic spike trains. In the
following, all averages denoted by
. The
output rate, however, was a deterministic function of the neuronal input. In
the context of spike-time dependent plasticity, we consider the set of
presynaptic spike arrival times
(tj1, tj2,...) as a random variable.
The underlying `randomness' may have several reasons. For example, different
stimulation paradigms may be selected one by one in very much the same way as
we have selected a new input pattern in the previous section. In contrast to
the rate model, we do not want to restrict ourselves to deterministic neuron
models. Hence, the randomness can also be produced by a stochastic neuron
model that is used in order account for noise; cf. Chapter 5. In this
case, the output spike train can be a random variable even if the input spike
trains are fixed. A simple example is the Poisson neuron model that generates
output spikes via an inhomogeneous Poisson process with an intensity that is a
function of the membrane potential. In any case, we consider the set of spike
trains
(S1,..., Si, Sj,..., SN), i.e., pre- and postsynaptic
trains, to be drawn from a stochastic ensemble. The specific properties of the
chosen neuron model are thus implicitly described by the association of pre-
and postsynaptic trains within the ensemble. Note that this formalism includes
deterministic models as a special case, if the ensemble contains only a single
postsynaptic spike train for any given set of presynaptic spike trains. In the
following, all averages denoted by
![]() .
. ![]() are to be taken
relative to this ensemble.
are to be taken
relative to this ensemble.
For the time being we are interested only in the long-term behavior of the synaptic weights and not in the fluctuations that are caused by individual spikes. As in Section 11.1.2 we therefore calculate the expectation value of the weight change over a certain interval of time,
| (11.38) |
| (11.39) |
The instantaneous firing rate ![]() (t) of neuron i is the
ensemble average of its spike train,
(t) of neuron i is the
ensemble average of its spike train,
| (11.42) |
Since averaging is a linear operations we can exchange ensemble average and time average. We obtain the following expression for the expected weight change in the interval from t to t + T as a function of the statistical properties of the spike trains,
The time average
![]()
![]() (t - s, t)
(t - s, t)![]() is the correlation
function of pre- and postsynaptic spike train on
the interval [t, t + T]. This function clearly depends on the actual value of
the weight vector. In deriving Eq. (11.49) we already had to assume that the
correlations are a slowly varying function of time. For the sake of
consistency we thus have the requirement that the weight vector itself is a
slowly varying function of time. If this is the case then we can exploit the
self-averaging property of the weight vector and argue that fluctuations
around the expectation value are negligible and that Eq. (11.49) is a good
approximation for the actual value of the weight vector. We thus drop the
ensemble average on the left-hand side of Eq. (11.49) and find for the
time-averaged change of the synaptic weight the following learning equation,
is the correlation
function of pre- and postsynaptic spike train on
the interval [t, t + T]. This function clearly depends on the actual value of
the weight vector. In deriving Eq. (11.49) we already had to assume that the
correlations are a slowly varying function of time. For the sake of
consistency we thus have the requirement that the weight vector itself is a
slowly varying function of time. If this is the case then we can exploit the
self-averaging property of the weight vector and argue that fluctuations
around the expectation value are negligible and that Eq. (11.49) is a good
approximation for the actual value of the weight vector. We thus drop the
ensemble average on the left-hand side of Eq. (11.49) and find for the
time-averaged change of the synaptic weight the following learning equation,
It is tempting to rewrite the correlation term
![]()
![]() (t - s, t)
(t - s, t)![]() that appears on the right-hand side of
Eq. (11.50) in terms of the instantaneous firing rates
that appears on the right-hand side of
Eq. (11.50) in terms of the instantaneous firing rates
![]()
![]() (t - s)
(t - s) ![]() (t)
(t)![]() . This, however, is only
allowed, if the spike trains of neuron i and j were independent, i.e., if
. This, however, is only
allowed, if the spike trains of neuron i and j were independent, i.e., if
![]() Si(t - s) Sj(t)
Si(t - s) Sj(t)![]() =
= ![]() Si(t - s)
Si(t - s)![]()
![]() Sj(t)
Sj(t)![]() . Such an approach would therefore
neglect the specific spike-spike correlations
that are induced by presynaptic action potentials.
. Such an approach would therefore
neglect the specific spike-spike correlations
that are induced by presynaptic action potentials.
Correlations between pre- and postsynaptic spike trains do not only depend on
the input statistics but also on the dynamics of the neuron model and the way
new output spikes are generated. The influence of a single presynaptic
spike on the postsynaptic activity can be measured by a peri-stimulus time
histogram (PSTH) triggered on the time of presynaptic spike arrival; cf.
Section 7.4.1. The form of the PSTH characterizes the
spike-spike correlations between presynaptic spike arrival and postsynaptic
action potential. For high noise, the spike-spike correlations contain a term
that is proportional to the time-course of the postsynaptic potential
![]() , while for low noise this term is proportional to its derivative
, while for low noise this term is proportional to its derivative
![]() ; cf. Figs. 7.12.
; cf. Figs. 7.12.
In the following, we will calculate the spike-spike correlations in a
particularly simple case, the linear Poisson neuron model. As we will see,
the spike-spike correlations contain in this case a term proportional to the
postsynaptic potential ![]() . The linear Poisson neuron model can
therefore be considered as a reasonable approximation to spiking neuron models
in the high-noise limit.
. The linear Poisson neuron model can
therefore be considered as a reasonable approximation to spiking neuron models
in the high-noise limit.
As a generalization of the analog neuron
with linear gain function discussed in Section 11.1.2 we consider
here a linear Poisson neuron.
The input to the neuron consists of N Poisson
spike trains with time-dependent intensities ![]() (t). Similar to the
SRM0 neuron the membrane potential ui of neuron i is a superposition
of postsynaptic potentials
(t). Similar to the
SRM0 neuron the membrane potential ui of neuron i is a superposition
of postsynaptic potentials ![]() with
with
![]()
![]() (s) ds = 1,
(s) ds = 1,
| ui(t) = |
(11.45) |
Postsynaptic spikes are generated by an inhomogeneous Poisson process with an
intensity
![]() that is a (semi-)linear function of
the membrane potential,
that is a (semi-)linear function of
the membrane potential,
| (11.46) |
We thus have a doubly stochastic process
(Bartlett, 1963; Cox, 1955)
in the sense that in a first step, a set
of input spike trains is drawn from an ensemble characterized by Poisson rates
![]() . This realization of input spike trains then determines
the membrane potential which produces in a second step a specific realization
of the output spike train according to
. This realization of input spike trains then determines
the membrane potential which produces in a second step a specific realization
of the output spike train according to
![]() (t| u). It can be
shown that,
because of the finite duration of the postsynaptic potential
(t| u). It can be
shown that,
because of the finite duration of the postsynaptic potential ![]() ,
the output spike trains generated by this composite process are no
longer Poisson spike trains; their expectation value
,
the output spike trains generated by this composite process are no
longer Poisson spike trains; their expectation value
![]() Si(t)
Si(t)![]()
![]()
![]() (t), however, is simply equivalent to the
expectation value of the output rate,
(t), however, is simply equivalent to the
expectation value of the output rate,
![]() (t) =
(t) = ![]()
![]() (t| u)
(t| u)![]() (Kistler and van Hemmen, 2000a). Due to the linearity of
the neuron model the output rate is given by a convolution of the input rates
with the response kernel
(Kistler and van Hemmen, 2000a). Due to the linearity of
the neuron model the output rate is given by a convolution of the input rates
with the response kernel ![]() ,
,
The joint firing rate
![]() (t, t') =
(t, t') = ![]() Si(t) Sj(t')
Si(t) Sj(t')![]() of pre- and postsynaptic neuron is the joint probability
density to find an input spike at synapse j at time t' and an output spike
of neuron i at time t. According to Bayes' Theorem this probability
equals the probability of observing an input spike at time t' times the
conditional probability of observing an output spike at time t given the
input spike at time t', i.e.,
of pre- and postsynaptic neuron is the joint probability
density to find an input spike at synapse j at time t' and an output spike
of neuron i at time t. According to Bayes' Theorem this probability
equals the probability of observing an input spike at time t' times the
conditional probability of observing an output spike at time t given the
input spike at time t', i.e.,
| (11.48) |
In the framework of a linear Poisson neuron, the term
![]() Si(t)| input spike att'
Si(t)| input spike att'![]() equals the sum of the expected
output rate (11.53) and the specific contribution
wij
equals the sum of the expected
output rate (11.53) and the specific contribution
wij ![]() (t - t') of a single (additional) input spike at time
t'. Altogether we obtain
(t - t') of a single (additional) input spike at time
t'. Altogether we obtain
If we use the result from Eq. (11.55) in the learning equation (11.50) we obtain
In linear Poisson neurons, the correlation between pre- and postsynaptic activity that drives synaptic weight changes consists of two contributions. The integral over the learning window in Eq. (11.56) describes correlations in the instantaneous firing rate. The last term on the right-hand side of Eq. (11.56) finally accounts for spike-spike correlations of pre- and postsynaptic neuron.
If we express the
instantaneous firing rates ![]() (t) in terms of their fluctuations
(t) in terms of their fluctuations
![]()
![]() (t) around the mean
(t) around the mean
![]()
![]() (t)
(t)![]() ,
,
| (11.50) |
The term containing Qkj(t) on the right-hand side of
Eq. (11.58) shows how spatio-temporal correlations
![]()
![]()
![]() (t')
(t') ![]()
![]() (t)
(t)![]() in the input influence the evolution of synaptic weights. What
matters are correlations on the time scale of the learning window and the
postsynaptic potential.
in the input influence the evolution of synaptic weights. What
matters are correlations on the time scale of the learning window and the
postsynaptic potential.
In Section 11.1.2 we have investigated the weight dynamics in the context of an analog neuron where the postsynaptic firing rate is an instantaneous function of the input rates. We have seen that learning is driven by (spatial) correlations within the set of input patterns. The learning equation (11.56) goes one step further in the sense that it explicitly includes time. Consequently, learning is driven by spatio-temporal correlations in the input.
In order to compare the rate-based learning paradigm of
Section 11.1.2 with the spike-based formulation of
Eq. (11.56) we thus have to disregard temporal correlations for
the time being. We thus consider a linear Poisson neuron with stationary
input rates,
![]()
![]() (t)
(t)![]() =
= ![]() (t) =
(t) = ![]() , and assume that the
synaptic weight is changing slowly as compared to the width of the learning
window and the postsynaptic potential. The weight dynamics is given by
Eq. (11.56),
, and assume that the
synaptic weight is changing slowly as compared to the width of the learning
window and the postsynaptic potential. The weight dynamics is given by
Eq. (11.56),
| c0(wij) = a0 , c1pre(wij) = a1pre + wij(t) W- , c1post(wij) = a1post , | (11.53) |
We may wonder what happens if we relax the requirement of strictly stationary rates. In the linear Poisson model, the output rate depends via Eq. (11.53) on the input rates and changes in the input rate translate into changes in the output rate. If the rate of change is small, we can expand the output rate
| (11.55) |
As compared to Eq. (11.60) we encounter an
additional term that is proportional to the first moment
![]() s W(s) ds of the learning window. This term has been termed differential-Hebbian (Roberts, 1999; Xie and Seung, 2000) and plays a certain role in
the context of conditioning and reinforcement learning
(Rao and Sejnowski, 2001; Montague et al., 1995).
s W(s) ds of the learning window. This term has been termed differential-Hebbian (Roberts, 1999; Xie and Seung, 2000) and plays a certain role in
the context of conditioning and reinforcement learning
(Rao and Sejnowski, 2001; Montague et al., 1995).
Another interesting property of a learning rule of the form (10.2) or (11.60) is that it can lead to a normalization of the postsynaptic firing rate and hence to a normalization of the sum of the synaptic weights. This can be achieved even without including higher order terms in the learning equation or postulating a dependence of the parameters a0, a1pre/post, etc., on the actual value of the synaptic efficacy.
Consider a linear Poisson neuron that receives input from N
presynaptic neurons with spike activity described by independent Poisson
processes with rate
![]() . The postsynaptic neuron is thus firing
at a rate
. The postsynaptic neuron is thus firing
at a rate
![]() (t) =
(t) = ![]()
![]() wij(t). From
Eq. (11.56) we obtain the corresponding dynamics for the
synaptic weights, i.e.,
wij(t). From
Eq. (11.56) we obtain the corresponding dynamics for the
synaptic weights, i.e.,
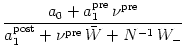 . . |
(11.58) |
In order to illustrate the above results with a concrete example we revisit
the static-pattern scenario that we have already studied in the context of
analog neurons in Section 11.1.2. We consider a set of static
patterns
{![]() ;1 <
;1 < ![]() < p} that are presented to the network in a
random sequence
(
< p} that are presented to the network in a
random sequence
(![]() ,
,![]() ,...) during time steps of length
,...) during time steps of length ![]() t.
Presynaptic spike trains are described by an inhomogeneous Poisson process
with a firing intensity that is determined by the pattern that is currently
presented. Hence, the instantaneous presynaptic firing rates are piecewise
constant functions of time,
t.
Presynaptic spike trains are described by an inhomogeneous Poisson process
with a firing intensity that is determined by the pattern that is currently
presented. Hence, the instantaneous presynaptic firing rates are piecewise
constant functions of time,
| (11.59) |
For linear Poisson neurons the joint firing rate of pre- and postsynaptic neuron is given by Eq. (11.55),
| (11.60) |
| = |
||
| (11.61) |
As usual, we are interested in the long-term behavior of the synaptic
weights given by Eq. (11.56). We thus need the
time-average of
![]() (t - s)
(t - s) ![]() (t) over the interval
T,
(t) over the interval
T,
| = |
(11.62) |
| (11.64) |
| = |
(11.65) |
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...
{\bf B}
\par\includegraphics[width=\textwidth]{stat_pat_b.eps}
\end{minipage}](img1941.gif) |
In order to understand this result let us first consider the case where both
the width of the learning window and the postsynaptic potential is small as
compared to the duration ![]() t of one pattern presentation. The integral
over s' in the definition of the matrix Qkj is the convolution of
t of one pattern presentation. The integral
over s' in the definition of the matrix Qkj is the convolution of
![]() with a triangular function centered around s = 0 that has a maximum
value of unity. Since
with a triangular function centered around s = 0 that has a maximum
value of unity. Since ![]() is normalized, the convolution yields a
smoothed version of the originally triangular function that is approximately
equal to unity in a neighborhood of s = 0; cf. Fig. 11.9B. If the
learning window is different from zero only in this neighborhood, then the
integral over s in Eq. (11.74) is just
is normalized, the convolution yields a
smoothed version of the originally triangular function that is approximately
equal to unity in a neighborhood of s = 0; cf. Fig. 11.9B. If the
learning window is different from zero only in this neighborhood, then the
integral over s in Eq. (11.74) is just ![]() , the area under the learning
window. We can thus collect the first two terms on the right-hand side of
Eq. (11.73) and obtain
, the area under the learning
window. We can thus collect the first two terms on the right-hand side of
Eq. (11.73) and obtain
| = |
(11.67) |
More interesting is the case where the time scale of the learning window is of
the same order of magnitude as the presentation of an input
pattern. In this case, the integral over s in Eq. (11.74) is
different from ![]() and we can choose a time window with
and we can choose a time window with ![]() = 0 so
that the first term on the right-hand side of Eq. (11.73)
vanishes. In this case, the weight dynamics is no longer determined by
= 0 so
that the first term on the right-hand side of Eq. (11.73)
vanishes. In this case, the weight dynamics is no longer determined by
![]()
![]()
![]()
![]() but by the matrix Qjk,
but by the matrix Qjk,
| = |
(11.68) |
| Qkj |
(11.69) |
If we assume that all presynaptic neurons have the same mean activity,
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() then we can rewrite Eq. (11.76) as
then we can rewrite Eq. (11.76) as
If spike arrival times are described as a stochastic process, the weight vector itself is also a random variable that evolves along a fluctuating trajectory. In Section 11.2.1, we have analyzed the expectation value of the synaptic weights smoothed over a certain interval of time. In the limit where the synaptic weights evolve much slower than typical pre- or postsynaptic interspike intervals, an approximation of the weight vector by its expectation values is justified. However, if the synaptic efficacy can be changed substantially by only a few pre- or postsynaptic spikes then the fluctuations of the weights have to be taken into account. Here, we are investigate the resulting distribution of synaptic weights in the framework of a Fokker-Planck equation (Rubin et al., 2001; van Rossum et al., 2000).
![\hbox{\hspace{10mm}
\includegraphics[width=70mm]{Figs-ch-hebb-anal/Fig-FP-transitions.eps}
\hspace{25mm}
}](img1946.gif) |
We consider a single neuron i that receives input from several hundreds of
presynaptic neurons. All presynaptic neurons fire independently at a
common constant rate
![]() . We are interested in the probability
density P(w, t) for the synaptic weight of a given synapse.
We assume that all weights are restricted to the interval
[0, wmax] so
that the normalization
. We are interested in the probability
density P(w, t) for the synaptic weight of a given synapse.
We assume that all weights are restricted to the interval
[0, wmax] so
that the normalization
![]() P(w, t) dw = 1 holds.
Weight changes due to potentiation or depression of
synapses induce changes in the density function P(w, t). The Fokker-Planck
equation that we will derive below describes the evolution of the distribution
P(w, t) as a function of time; cf. Fig. 11.10.
P(w, t) dw = 1 holds.
Weight changes due to potentiation or depression of
synapses induce changes in the density function P(w, t). The Fokker-Planck
equation that we will derive below describes the evolution of the distribution
P(w, t) as a function of time; cf. Fig. 11.10.
For the sake of simplicity, we adopt a learning window with two rectangular phases, i.e.,
W(s) = 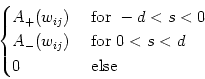 |
(11.71) |
There are basically two possibilities to restrict the synaptic weights to the
interval
[0, wmax]; we can either impose hard or soft bounds to the
weight dynamics; cf. Section 10.2.1. Hard
bounds means that the weights are simply
no longer increased (decreased) if the upper (lower) bound is reached. Soft
bounds, on the other hand, gradually slow
down the evolution if the weight approaches one of its bounds. A simple way to
implement soft bounds in our formalism is to define (Kistler and van Hemmen, 2000a)
| A+(wij) | = | (wmax - wij) a+ , | (11.72) |
| A-(wij) | = | - wij a- , | (11.73) |
![\hbox{{\bf A} \hspace{60mm} {\bf B}} \hbox{\hspace{10mm}
\includegraphics[width...
...5mm}
\includegraphics[width=50mm]{Figs-ch-hebb-anal/Fig-FP-window-c_new.eps} }](img1949.gif) |
In order to derive the evolution of the distribution P(w, t) we consider transitions in the `weight space' induced by pre- and postsynaptic spike firing. The evolution is described by a master equation of the form
| = - p+(w) P(w, t) - p-(w) P(w, t) | (11.74) | |
+  |
||
+  |
| (11.75) |
| p+(w, t) | = |
(11.76) |
| p-(w, t) | = |
(11.77) |
Equation (11.82) can be rewritten in the form of a Fokker-Planck equation if we expand the right-hand side to second order in the transition amplitudes A+ and A- (van Kampen, 1992),
| A(w, t) | = p+(w, t) A+(w) - p-(w, t) A-(w) , | (11.79) |
| B(w, t) | = p+(w, t) A+2(w) - p-(w, t) A-2(w) . | (11.80) |
![\hbox{{\bf A} \hspace{60mm} {\bf B}} \hbox{\hspace{10mm}
\includegraphics[width...
...hspace{25mm}
\includegraphics[width=50mm]{Figs-ch-hebb-anal/Fig-FP-P0-b.eps} }](img1956.gif) |
The Fokker-Planck equation (11.86) can be solved numerically to find stationary solutions. It turns out that the qualitative form of the distribution depends critically on how the bounds for the weights are implemented; cf. Rubin et al. (2001); van Rossum et al. (2000) for details. With soft bounds the distribution is unimodal whereas with hard bounds it peaks at both borders of the interval; cf. Fig. 11.12. Experimental data suggests a unimodal distribution, consistent with soft bounds (van Rossum et al., 2000).
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.