![\centerline{\includegraphics[width=10cm]{timewindow.eps}}](img1364.gif) |
In many areas of the brain synaptic projections form so-called reverberating loops. Neurons from one cortical area innervate an anatomically distinct nucleus that in turn projects back to the cortex in a topographically organized fashion. A prominent example is the olivo-cerebellar system. The inferior olive (IO) is a nucleus in the brain stem that is part of a reverberating loop formed by the cerebellar cortex and the deep cerebellar nuclei. A single round-trip from the IO to the cerebellar cortex, the deep cerebellar nuclei, and back to the olive takes about 100 ms - a rather long delay that is the result of slow synaptic processes, in particular of post-inhibitory rebound firing; cf. Chapter 2.3.3. It is known that IO neurons tend to fire synchronously at about 10 Hz which is due to sub-threshold oscillations of the membrane potential (Bell and Kawasaki, 1972; Sotelo et al., 1974; Llinás and Yarom, 1986; De Zeeuw et al., 1998) and an exceptionally high density of gap junctions. The delayed feedback can thus give rise to oscillations of the population activity in the olive. Analogously organized projections together with 10 Hz oscillations (the so-called theta rhythm) can also be observed in other areas of the brain including the olfactory system, hippocampus, and cortico-thalamic loops.
In the previous sections of this chapter we have dealt with networks that exhibit regular oscillations of the neuronal activity. On the other hand, experiments show that though oscillations are a common phenomenon, spike trains of individual neurons are often highly irregular. Here we investigate the question whether these observations can be reconciled: Is it possible to have a periodic large-amplitude oscillation of the population activity and at the same time irregular spike trains? The answer is positive, provided that individual neurons fire with an average frequency that is significantly lower than the frequency of the population activity. Similarly to the cluster states discussed above, each neuron fires on average only in, say, one out of ten cycles of the population activity - the composition of the clusters of synchronously firing neurons, however, changes from cycle to cycle resulting in a broad distribution of inter-spike intervals; cf. Section 8.1. This is exactly what has been observed in the inferior olive. Individual neurons have a low firing rate of one spike per second; the population activity, however, oscillates at about 10 Hz; cf. Fig. 8.11.
![\centerline{\includegraphics[width=10cm]{timewindow.eps}}](img1364.gif) |
We are particularly interested in the effect of feedback projections on the generated spike patterns. In keeping with experimental findings we assume that the feedback projections are sparse, i.e., that spikes from a given neuron in one cycle affect only a small portion of the whole population during the next cycle. Hence, we drop the assumption of an all-to-all connectivity and use randomly connected networks instead. It turns out that irregular spike trains can indeed be generated by the ``frozen noise'' of the network connectivity; cf. Chapter 6.4.3. Since the connectivity is random but fixed the spike patterns of noiseless neurons are fully deterministic though they look irregular. Strong oscillations with irregular spike trains have interesting implications for short-term memory and timing tasks (Billock, 1997; Kistler and De Zeeuw, 2002; Nützel et al., 1994).
This chapter is dedicated to an investigation of the dynamical properties of neuronal networks that are part of a reverberating loop. We assume that the feedback is in resonance with a T-periodic oscillation of the population activity and that the neurons stay synchronized, i.e., fire only during narrow time windows every T milliseconds. We furthermore assume that the set of neurons that is active in each cycle depends only on the synaptic input that is due to the reverberating loop and thus depends only on the activity of the previous cycle. With these assumptions it is natural to employ a time-discrete description based on McCulloch-Pitts neurons. Each time step corresponds to one cycle of length T. The wiring of the reverberating loop is represented by a random coupling matrix. The statistical properties of the coupling matrix reflect the level of divergence and convergence within the reverberating network.
We have seen that - depending on the noise level - a network can reach a
state where all neurons are firing in lockstep. Such a large-amplitude
oscillation implies that neurons do only fire only during short time windows
around
t ![]() n T. Whether or not a neuron fires within the `allowed'
time window depends on the input it receives from other neurons in the
population.
n T. Whether or not a neuron fires within the `allowed'
time window depends on the input it receives from other neurons in the
population.
The membrane potential for SRM0 neurons is given by
With these assumptions, the dynamics of the spiking neuron model
(8.31) reduces to a binary model in discrete time (McCulloch and Pitts, 1943).
Let us set
tn = n T and introduce binary variables
Si ![]() {0, 1} for
each neuron indicating whether neuron i is firing a spike at
ti(f)
{0, 1} for
each neuron indicating whether neuron i is firing a spike at
ti(f) ![]() tn or not. Equation (8.31) can thus be rewritten as
tn or not. Equation (8.31) can thus be rewritten as
The reduction of the spiking neuron model to discrete time and binary neurons allows us to study oscillations with irregular spike trains in a transparent manner. In a first step we derive mean field equations and discuss their macroscopic behavior. In a second step we look more closely into the microscopic dynamics. It will turn out that subtle changes in the density of excitatory and inhibitory projections can have dramatic effects on the microscopic dynamics that do not show up in a mean field description. Binary discrete-time models with irregular spike trains have been studied in various contexts by (Kirkpatrick and Sherrington, 1978), Derrida et al. (1987), Crisanti and Sompolinsky (1988), Nützel (1991), Kree and Zippelius (1991), van Vreeswijk and Sompolinsky (1996) to mention only a few. As we have seen above, strong oscillations of the population activity provide a neuronal clocking mechanism and hence a justification of time-discretization.
We consider a population of N McCulloch-Pitts neurons (McCulloch and Pitts, 1943)
that is described by a state vector
![]()
![]() {0, 1}N. In each time step
tn any given neuron i is either active [
Si(tn) = 1] or inactive
[
Si(tn) = 0]. Due to the reverberating loop, neurons receive (excitatory)
synaptic input h that depends on the wiring of the loop - described by a
coupling matrix wij - and on the activity during the previous cycle, i.e.,
{0, 1}N. In each time step
tn any given neuron i is either active [
Si(tn) = 1] or inactive
[
Si(tn) = 0]. Due to the reverberating loop, neurons receive (excitatory)
synaptic input h that depends on the wiring of the loop - described by a
coupling matrix wij - and on the activity during the previous cycle, i.e.,
| prob{wij = 1} = |
The neurons are modeled as deterministic threshold elements. The dynamics is given by
Starting with a random initial firing pattern,
| Si(t0) |
The dynamics of the population activity is completely characterized by the
mean field equation (8.40). For instance, it can easily be shown
that an = 0 is a stable fixed point except if
![]() = 1 and
= 1 and
![]() > 1. Furthermore, an is a monotonously growing function of
an-1. Therefore, no macroscopic oscillations can be expected. In summary,
three different constellations can be discerned; cf. Fig. 8.12. First, for
> 1. Furthermore, an is a monotonously growing function of
an-1. Therefore, no macroscopic oscillations can be expected. In summary,
three different constellations can be discerned; cf. Fig. 8.12. First, for
![]() = 1 and
= 1 and ![]() > 1 there is a stable fixed point
at high levels of an; the fixed point at an = 0 is unstable. Second, if
the firing threshold
> 1 there is a stable fixed point
at high levels of an; the fixed point at an = 0 is unstable. Second, if
the firing threshold ![]() is large as compared to the convergence
is large as compared to the convergence
![]() only an = 0 is stable. Finally, if
only an = 0 is stable. Finally, if
![]() > 1 and
> 1 and ![]() sufficiently large, bistability of an = 0 and an > 0 can be observed.
sufficiently large, bistability of an = 0 and an > 0 can be observed.
![\begin{minipage}{0.3\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]{...
...[clip=true,width=\textwidth,trim=0 0 0 13]{reverb_sim_8_4.ps.gz}
\end{minipage}](img1375.gif) |
In a network with purely excitatory interactions
the non-trivial fixed point corresponds
to a microscopic state where some neurons are active and others
inactive. Since the active neurons fire
at practically every cycle of the oscillation,
we do not find the desired broad distribution
of interspike intervals;
cf. Fig. 8.12A.
As we have already seen in
Chapter 6.4.3,
a random network with balanced excitation and inhibition
is a good candidate for generating broad interval distributions.
Reverberating projections are, in fact, not
necessarily excitatory. Instead, they are
often paralleled by an inhibitory pathway that may either involve another
brain region or just inhibitory interneurons.
Our previous model can easily be extended so as to account both for excitatory
and inhibitory projections. The wiring of the excitatory loop is
characterized, as before, by a random matrix
wijexc ![]() {0, 1}
with
{0, 1}
with
| prob{wijexc = 1} = |
| prob{wijinh = 1} = |
Let us assume that a neuron is activated if the difference between excitatory
and inhibitory input exceeds its firing threshold ![]() . The dynamics is
thus given by
. The dynamics is
thus given by
As compared to the situation with purely excitatory feedback Eq. (8.44) does not produce new modes of behavior. The only difference is that an+1 is no longer a monotonous function of an; cf. Fig. 8.13.
![\begin{minipage}{0.3\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]{...
...[width=\textwidth,trim=0 10 0 10]{reverb_sim_10_4_3_subtr.ps.gz}
\end{minipage}](img1386.gif) |
As it is already apparent from the examples shown in Figs. 8.12 and 8.13 the irregularity of the spike trains produced by different reverberating loops can be quite different. Numerical experiments show that in the case of purely excitatory projections fixed points of the mean field dynamics almost always correspond to a fixed point of the microscopic dynamics, or at least to a limit cycle with short period. As soon as inhibitory projections are introduced this situation changes dramatically. Fixed points in the mean field dynamics still correspond to limit cycles in the microscopic dynamics; the length of the periods, however, is substantially larger and grows rapidly with the network size; cf. Fig. 8.14 (Nützel, 1991; Kirkpatrick and Sherrington, 1978). The long limit cycles induce irregular spike trains which are reminiscent of those found in the asynchronous firing state of randomly connected integrate-and-fire network; cf. Chapter 6.4.3.
![\begin{minipage}{0.49\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...
\par\includegraphics[width=\textwidth]{max_attractor_length.ps}
\end{minipage}](img1387.gif) |
With respect to potential applications it is particularly interesting to see how information about the initial firing pattern is preserved in the sequence of patterns generated by the reverberating network. Figure 8.15A shows numerical results for the amount of information that is left after n iterations. At t = 0 firing is triggered in a subset of neurons. After n iterations, the patterns of active neurons may be completely different. The measure In/I0 is the normalized transinformation between the initial pattern and the pattern after n iterations. In/I0 = 1 means that the initial pattern can be completely reconstructed from the activity pattern at iteration n; In/I0 = 0 means that all the information is lost.
Once the state of the network has reached a limit cycle it will stay there forever due to the purely deterministic dynamics given by Eq. (8.36), or (8.43). In reality, however, the presence of noise leads to mixing in the phase space so that the information about the initial state will finally be lost. There are several sources of noise in a biological network - the most prominent are uncorrelated ``noisy'' synaptic input from other neurons and synaptic noise caused by synaptic transmission failures.
Figure 8.15B shows the amount of information about the initial pattern that is left after n iterations in the presence of synaptic noise in a small network with N = 16 neurons. As expected, unreliable synapses lead to a faster decay of the initial information. A failure probability of 5 percent already leads to a significantly reduced capacity. Nevertheless, a failure rate of 5 percent leaves after 5 iterations more than 10 percent of the information about the initial pattern; cf. Fig. 8.15B. This means that 10 neurons are enough to discern two different events half a second - given a 10 Hz oscillation - after they actually occurred. Note that this is a form of ``dynamic short-term memory'' that does not require any form of synaptic plasticity. Information about the past is implicitly stored in the neuronal activity pattern. Superordinated neurons can use this information to react with a certain temporal relation to external events (Billock, 1997; Kistler and De Zeeuw, 2002; Kistler et al., 2000).
![\begin{minipage}{0.45\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]...
...f B}
\par\includegraphics[width=\textwidth]{transinfo_noise.eps}
\end{minipage}](img1388.gif) |
Information theory (Cover and Thomas, 1991; Shannon, 1948; Ash, 1990) provides us with valuable tools to quantify the amount of ``uncertainty'' contained in a random variable and the amount of ``information'' that can be gained by measuring such a variable. Consider a random variable X that takes values xi with probability p(xi). The entropy H(X),
If we have two random variables X and Y with joint probability p(xi, yj) then we can define the conditioned entropy H(Y| X) that gives the (remaining) uncertainty for Y given X,
H(Y| X) = - 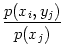 . . |
(8.42) |
In order to produce Fig. 8.15 we have generated random
initial patterns ![]() together with the result of the iteration,
together with the result of the iteration,
![]() , and incremented the corresponding counters in a large (
216×216) table so as to estimate the joint probability distribution of
, and incremented the corresponding counters in a large (
216×216) table so as to estimate the joint probability distribution of
![]() and
and ![]() . Application of Eq. (8.45)-Eq. (
. Application of Eq. (8.45)-Eq. (![]() ) yields Fig. 8.15.
) yields Fig. 8.15.
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.