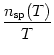 |
(5.125) |
All neuron models considered up to now emit spikes, either explicit action potentials that are generated by ionic processes as in Chapter 2, or formal spikes that a generated by a threshold process as in Chapter 4. On the other hand, if we take the point of view of rate coding, single spikes of individual neurons do not play an important role; cf. Chapter 1.4. The essential quantity to be transmitted from one group of neurons to the next is the firing rate, defined either as a temporal or as a population average. If this is true, models formulated on the level of firing rates would be sufficient.
As we have seen in Chapter 1.4, there are several ways to define the firing rate of a neuron. Consequently, rate-based models differ with respect to their notion of `firing rate'. Here we focus on three different rate models, viz., analog neurons (averaging over time), stochastic rate models (averaging over a stochastic ensemble), and population rate models (averaging over a population of neurons).
If rate coding is understood in the sense of a spike count, then the essential information is carried by the mean firing rate, defined by the number nsp(T) of spikes that occur in a given time interval T divided by T
We have seen in the previous chapters that a neuron that is driven by a
constant intracellular current I0, emits a regular spike train. The rate
![]() is then simply the inverse of the constant interspike interval s. If
the drive current I0 is increased, the mean firing rate increases as well
until it saturates at a maximum rate
is then simply the inverse of the constant interspike interval s. If
the drive current I0 is increased, the mean firing rate increases as well
until it saturates at a maximum rate
![]() . The relation g
between the output rate and the input,
. The relation g
between the output rate and the input,
![\begin{minipage}{0.3\textwidth}
{\bf A}
\par\includegraphics[width=\textwidth]{...
...\par\includegraphics[width=\textwidth]{pout.dat.gain-linear.eps}
\end{minipage}](img943.gif) |
In a network of neurons in rate description, the input Ii to a neuron i
is generated by the rates ![]() of other neurons j. Typically it is
assumed that Ii is just a weighted sum,
of other neurons j. Typically it is
assumed that Ii is just a weighted sum,
We refer to the variable ![]() as the firing rate or
activation of neuron i. The interpretation of the input Ii is somewhat
ambiguous. Some modelers think of it as a current, consistent with our
notation in Eq. (5.127). Other researchers take Ii as a voltage and
call it the postsynaptic potential. In the case of constant input, the
interpretation is irrelevant, since the Eq. (5.128) is only used as a
phenomenological model of certain aspects of neural information processing.
The neuron itself is essentially treated as a black box which transforms a set
of input rates into an output rate.
as the firing rate or
activation of neuron i. The interpretation of the input Ii is somewhat
ambiguous. Some modelers think of it as a current, consistent with our
notation in Eq. (5.127). Other researchers take Ii as a voltage and
call it the postsynaptic potential. In the case of constant input, the
interpretation is irrelevant, since the Eq. (5.128) is only used as a
phenomenological model of certain aspects of neural information processing.
The neuron itself is essentially treated as a black box which transforms a set
of input rates into an output rate.
In formal models the transfer function is often described by a hyperbolic tangent,
For
![]()
![]()
![]() , the gain function (5.129) approaches a
step function
, the gain function (5.129) approaches a
step function
If we consider spike firing as a stochastic process we can think of
the firing rate ![]() also as the probability density of finding a spike at a
certain instance of time. In this picture,
also as the probability density of finding a spike at a
certain instance of time. In this picture, ![]() is the rate of the
underlying Poisson process that generates the spikes; cf.
Section 5.2.3. Stochastic rate models are therefore on
the border line between analog rate models and noisy spiking neuron models.
The main difference is that stochastic spiking neuron models such as the Spike
Response Model with escape noise (cf. Section 5.3) allows us to
include refractoriness whereas a Poisson model does not (Kistler and van Hemmen, 2000a).
is the rate of the
underlying Poisson process that generates the spikes; cf.
Section 5.2.3. Stochastic rate models are therefore on
the border line between analog rate models and noisy spiking neuron models.
The main difference is that stochastic spiking neuron models such as the Spike
Response Model with escape noise (cf. Section 5.3) allows us to
include refractoriness whereas a Poisson model does not (Kistler and van Hemmen, 2000a).
A stochastic rate model in continuous time is defined by an inhomogeneous
Poisson process. Spikes are formal events characterized by their firing time
tj(f) where j is the index of the neuron and f counts the
spikes. At each moment of time spikes are generated with rate ![]() (t)
which depends on the input. It is no longer possible to calculate the input
from a rate equation as in Eq. (5.127) since the input consists now of
spikes which are point events in time. We set
(t)
which depends on the input. It is no longer possible to calculate the input
from a rate equation as in Eq. (5.127) since the input consists now of
spikes which are point events in time. We set
| (5.132) |
| hi(t) = |
(5.133) |
In order to illustrate the relation with the deterministic rate model of
Eq. (5.128), we discretize time in steps of length
![]() t = 1/
t = 1/![]() where
where
![]() is the maximum firing rate. In each time step the stochastic
neuron is either active (
Si = + 1) or quiescent (Si = 0). The two
states are taken stochastically with a probability which depends continuously
upon the input hi. The probability that a neuron is active at time
t +
is the maximum firing rate. In each time step the stochastic
neuron is either active (
Si = + 1) or quiescent (Si = 0). The two
states are taken stochastically with a probability which depends continuously
upon the input hi. The probability that a neuron is active at time
t + ![]() t given an input hi at time t is
t given an input hi at time t is
| hi(t) = |
(5.135) |
Closely related to the stochastic point of view
is the notion of the rate as the average activity of a population of
equivalent neurons. `Equivalent' means that all neurons have identical
connectivity and receive the same type of input. Noise, however, is considered
to be independent for each pair of neurons so that their response to the input
can be different. We have seen in Section 1.5 that we can define
a `rate', if we take a short time window ![]() t, count the number of
spikes (summed over all neurons in the group) that occur in an interval
t...t +
t, count the number of
spikes (summed over all neurons in the group) that occur in an interval
t...t + ![]() t and divide by the number of neurons and
t and divide by the number of neurons and ![]() t. In the
limit of
N
t. In the
limit of
N![]()
![]() and
and
![]() t
t![]() 0 (in this order), the activity A
is an analog variable which varies in continuous time,
0 (in this order), the activity A
is an analog variable which varies in continuous time,
Let us assume that we have several groups of neurons. Each group l contains a large number of neurons and can be described by its activity Al. A simple phenomenological model for the interaction between different groups is
We will see later in Chapter 6, that Eq. (5.137) is indeed a correct description of the fixed point of interacting populations of neurons, that is, if all activity values Ak are, apart from fluctuations constant. As mentioned in Chapter 1.4, the interpretation of the rate as a population activity is not without problems. There are hardly ensembles which would be large enough to allow sensible averaging and, at the same time, consist of neurons which are strictly equivalent in the sense that the internal parameters and the input is identical for all the neurons belonging to the same ensemble. On the other hand, neurons in the cortex are often arranged in groups (columns) that are roughly dealing with the same type of signal and have similar response properties. We will come back to the interpretation of Eq. (5.137) as a population activity in Chapter 6.
The population rate does not require temporal averaging and can, in principle, change on a rapid time scale. A time-dependent version of the population rate equation (5.137) is the so-called Wilson-Cowan equation (Wilson and Cowan, 1972)
In order to derive Eq. (5.138), Wilson and Cowan had to make a couple
of strong assumptions and we may wonder whether (5.138) can be
considered a realistic description of the population dynamics. More
specifically, what determines the time constant ![]() which limits the
response time of the system? Is it given by the membrane time constant of a
neuron? Is
which limits the
response time of the system? Is it given by the membrane time constant of a
neuron? Is ![]() really constant or does it depend on the input or
the activity of the system? We will see in Chapter 6 that
the population activity of a group of spiking neurons can, in some
cases, react instantaneously to changes in the input. This suggests that the
`time constant'
really constant or does it depend on the input or
the activity of the system? We will see in Chapter 6 that
the population activity of a group of spiking neurons can, in some
cases, react instantaneously to changes in the input. This suggests that the
`time constant' ![]() in (5.138) is, at least in some cases, extremely
short. The theory of population dynamics developed in
Chapter 6 does not make use of the differential equation
(5.138), but uses a slightly different mathematical framework.
in (5.138) is, at least in some cases, extremely
short. The theory of population dynamics developed in
Chapter 6 does not make use of the differential equation
(5.138), but uses a slightly different mathematical framework.
© Cambridge University Press
This book is in copyright. No reproduction of any part
of it may take place without the written permission
of Cambridge University Press.